
����Ŀ��2016����������������������Ͷ��8ǧ��Ԫ����������պ����۹����μ��ջ���ҵ��Ŀ���滮��2017�������൱��������ÿ�����Ͷ��2ǧ��Ԫ���ڴ���Ŀ.2016�����Ŀ�ľ�����Ϊ5����Ԫ�������ξ�������ջ���ҵ�����룩����Ԥ�����൱��������ÿ��ľ������Ϊ��һ���1.5������2016��Ϊ��1�꣬f��n��Ϊ��1�����˺��n��n��N*������ۼ�����ע������n�꣬�ۼ�����=�ۼƾ����멁�ۼ�Ͷ�룬��λ��ǧ��Ԫ�����ҵ�f��n��Ϊ��ֵʱ����Ϊ����ĿӮ����
��1������f��n���ı���ʽ��
��2������Ԥ�⣬����Ŀ������һ�꿪ʼ������Ӯ������˵�����ɣ�
���ο����ݣ� ![]() ��ln2��0.7��ln3��1.1��
��ln2��0.7��ln3��1.1��
���𰸡�
��1���⣺������֪����1�����˺��n��n��N*������ۼ�Ͷ��
Ϊ8+2��n��1��=2n+6��ǧ��Ԫ��
��1�����˺��n��n��N*������ۼƾ�����
Ϊ ![]() =
= 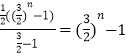 ��ǧ��Ԫ����
��ǧ��Ԫ����
���� ![]() ��ǧ��Ԫ��
��ǧ��Ԫ��
��2���⣺��Ϊ ![]() =
= ![]() ��
��
���Ե�n��3ʱ��f��n+1����f��n����0���ʵ�n��4ʱ��f��n���ݼ���
��n��4ʱ��f��n+1����f��n����0���ʵ�n��4ʱ��f��n��������
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
���ԣ�����Ŀ���ӵ�8�꿪ʼ������Ӯ����
�𣺸���Ŀ����2023�꿪ʼ������Ӯ����
����������1���������֪����1�����˺��n��n��N*������ۼƾ����룬�ǵȱ����У����õȱ�����ǰn���ʽ������ý������2������ָ�������ĵ����Լ�ֵ����ֵ���ɵõ������


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ǵȱ������Σ��߳�Ϊ4��BC�ߵ��е�ΪD����ԲW��A��DΪ���������㣬�Ҿ���B��C���㣮
��1�������Բ�ı����̣�
��2������D��x���ֱ��ֱ��l����Բ��M��N���㣬��֤��ֱ��BM��CN�Ľ�����һ����ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵĺ���y=f��x��������f��x��=f��2��x����������f�䣨x����x��1����0���������x1��x2 �� ��f��x1����f��x2�������ij�Ҫ�����ǣ� ��
A.x2��x1��1
B.x1+x2��2
C.x1+x2��2
D.x2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к��������溯�����ڣ�0��+�ޣ��ϵ����ݼ����ǣ� ��
A.f��x��=x4
B.![]()
C.![]()
D.f��x��=x3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xlnx��x�� ![]() ��a��R�����ڶ���������������ͬ�ļ�ֵ��x1 �� x2��x1��x2����
��a��R�����ڶ���������������ͬ�ļ�ֵ��x1 �� x2��x1��x2����
�� I����a��ȡֵ��Χ��
�� II����֤��x1+x2��2e��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��ԲO��x2+y2=4�ϵĶ��㣬��A��4��0������ֱ��y=kx+1���ܴ��ڵ�Q��ʹ��Qǡ���߶�AP���е㣬��ʵ��k��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��ax��1��ex��a��0��e����Ȼ�����ĵ�������
��1��������f��x��������[1��2]���ǵ�������������ʵ��a��ȡֵ��Χ��
��2������f��x���ļ�ֵ��
��3���躯��f��x��ͼ��������һ�㴦������Ϊl����l��x���ϵĽؾ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0����a��1������f��x��=ax��1��g��x��=��x2+xlna��
��1����a��1��֤������h��x��=f��x����g��x�������䣨0��+�ޣ����ǵ�����������
��2������h��x��=f��x����g��x��������[��1��1]�ϵ����ֵ��
��3��������F��x����ͼ���ԭ�㣬��F�䣨x��=g��x������a��e ![]() ʱ������F��x������A��1��m��������������2������ʵ��m��ֵ��
ʱ������F��x������A��1��m��������������2������ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2+c��g��x��=aex��ͼ���һ��������ΪP��2��t����������y=f��x����y=g��x����P�㴦����ͬ�����ߣ�������f��x����g��x���ĸ���������䣨k��k+1����k��Z���ڣ���k= ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com