
【题目】在等比数列![]() 中,
中,
(1)已知![]() ,求
,求![]() 和
和![]() ;
;
(2)已知![]() ,求
,求![]() 和
和![]() ;
;
(3)已知![]() ,
,![]() ,求
,求![]() 和
和![]() ;
;
(4)已知![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)![]() ,
,![]() ;
;
(2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() 或
或![]() ,
, ;
;
(4)![]() .
.
【解析】
设等比数列![]() 的公比为
的公比为![]() .
.
(1)确定出等比数列![]() 的首项和公比,利用等比数列的前
的首项和公比,利用等比数列的前![]() 项和公式求出
项和公式求出![]() ,并求出
,并求出![]() ;
;
(2)利用![]() 求出
求出![]() ,再令
,再令![]() ,得出
,得出![]() ,再检验
,再检验![]() 是否满足
是否满足![]() ,由此可得出数列
,由此可得出数列![]() 的通项公式,并求出
的通项公式,并求出![]() 的值;
的值;
(3)利用首项和公比建立方程组,求出这两个量,然后利用等比数列的通项公式和前![]() 项和公式求出
项和公式求出![]() 和
和![]() ;
;
(4)分![]() 和
和![]() 两种情况,建立
两种情况,建立![]() 和
和![]() 的方程组,解出这两个量,然后利用等比数列的前
的方程组,解出这两个量,然后利用等比数列的前![]() 项和公式可求出
项和公式可求出![]() 的值.
的值.
设等比数列![]() 的公比为
的公比为![]() .
.
(1)![]() ,所以,数列
,所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,
因此, ,
,![]() ;
;
(2)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() 适合上式,所以,对任意的
适合上式,所以,对任意的![]() ,
,![]() ,因此,
,因此,![]() ;
;
(3)由 ,得
,得 ,解得
,解得![]() 或
或 .
.
当![]() 时,
时,![]() ,
,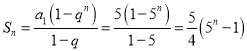 ;
;
当![]() ,
,![]() 时,
时,![]() ,
,
 ;
;
(4)当![]() 时,
时,![]() ,得
,得![]() ,
,
此时,![]() ,矛盾;
,矛盾;
当![]() 时,
时, ,
,
所以, ,解得
,解得 ,
,
因此, .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离A为
方向,距离A为![]() 海里的B处有一艘走私船,在A处北偏西
海里的B处有一艘走私船,在A处北偏西![]() 方向距离
方向距离![]() 为
为![]() 海里的
海里的![]() 处有我方一艘辑私艇奉命以
处有我方一艘辑私艇奉命以![]() 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以![]() 海里/小时的速度从
海里/小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,海岛O上有一座海拔300m的山,山顶上设有一个观察站A.上午11时测得一轮船在岛北偏东![]() 的B处,俯角为
的B处,俯角为![]() ;11时20分又测得该船在岛的北偏西
;11时20分又测得该船在岛的北偏西![]() 的C处,俯角为
的C处,俯角为![]() .
.

(1)该船的速度为每小时多少千米?
(2)若此船以不变的航速继续前进,则它何时到达岛的正西方向?此时船离开岛多少千米?(精确到lm)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼,它形象化的表达了阴阳轮转,相反相成是万物生成变化根源的哲理,展现了一种相互转化,相对统一的形式美.如图,按照太极图的构图方法,在平面直角坐标系中,圆![]() 被函数
被函数![]() 的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为
的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为![]() ,现在大圆内随机取一点,则此点取自阴影部分的概率为( )
,现在大圆内随机取一点,则此点取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型水果超市每天以![]() 元/千克的价格从水果基地购进若干
元/千克的价格从水果基地购进若干![]() 水果,然后以
水果,然后以![]() 元/千克的价格出售,若有剩余,则将剩下的水果以
元/千克的价格出售,若有剩余,则将剩下的水果以![]() 元/千克的价格退回水果基地,为了确定进货数量,该超市记录了
元/千克的价格退回水果基地,为了确定进货数量,该超市记录了![]() 水果最近
水果最近![]() 天的日需求量(单位:千克),整理得下表:
天的日需求量(单位:千克),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各日需求量的频率代替各日需求量的概率.
天记录的各日需求量的频率代替各日需求量的概率.
(1)求该超市![]() 水果日需求量
水果日需求量![]() (单位:千克)的分布列;
(单位:千克)的分布列;
(2)若该超市一天购进![]() 水果
水果![]() 千克,记超市当天
千克,记超市当天![]() 水果获得的利润为
水果获得的利润为![]() (单位:元),求
(单位:元),求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B、C、D为空间四个不共面的点,以![]() 的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com