练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数（）.

    （1）求的极值；

    （2）设,若当时,恒成立,求实数m的取值范围.

    【答案】（1）答案不唯一,具体见解析（2）

    【解析】

    (1)求导可得,再分与两种情况分别讨论导函数的正负以及原函数的单调性即可.

    (2)易得,再求导分析的单调性,进而求出最小值,再利用恒成立问题的方法解决即可.

    （1）由条件得的定义域为,（）.

    ①当时,,所以在上单调递增.

    ②当时,令,得（负值舍去）,

    因为当时,当时,,

    所以在上单调递减,在上单调递增.

    综上,①当时,无极值；

    ②当时,有极小值,无极大值.

    （2）当时,.

    设（）.

    则（）.

    令,得,

    因为当时,,当时,

    所以的单调递减区间为,单调递增区间为,

    所以的极小值也是最小值为

    因为在上恒成立,

    所以,即,

    故实数m的取值范围为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点的距离之比为定值的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系中,点.设点的轨迹为,下列结论正确的是（ ）

    A. 的方程为

    B. 在轴上存在异于的两定点,使得

    C. 当三点不共线时,射线是的平分线

    D. 在上存在点,使得

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆Γ：的左，右焦点分别为F1(，0)，F2(，0)，椭圆的左，右顶点分别为A，B，已知椭圆Γ上一异于A，B的点P，PA，PB的斜率分别为k1，k2，满足.

    （1）求椭圆Γ的标准方程；

    （2）若过椭圆Γ左顶点A作两条互相垂直的直线AM和AN，分别交椭圆Γ于M，N两点，问x轴上是否存在一定点Q，使得∠MQA=∠NQA成立，若存在，则求出该定点Q，否则说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面为正方形，且底面，过的平面与侧面的交线为，且满足（表示的面积）.

    （1）证明： 平面；

    （2）当时，二面角的余弦值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的顶点在坐标原点，准线方程为，为抛物线的焦点，点为直线上任意一点，以为圆心，为半径的圆与抛物线的准线交于、两点，过、分别作准线的垂线交抛物线于点、.

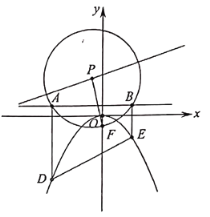
    （1）求抛物线的方程；

    （2）证明：直线过定点，并求出定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，圆：，定点，点是圆上一动点，线段的垂直平分线交圆的半径于点，点的轨迹为．

    （Ⅰ）求曲线的方程；

    （Ⅱ）不垂直于轴且不过点的直线与曲线相交于两点，若直线、的斜率之和为0，则动直线是否一定经过一定点？若过一定点，则求出该定点的坐标；若不过定点，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一款小游戏的规则如下：每轮游戏要进行三次，每次游戏都需要从装有大小相同的2个红球，3个白球的袋中随机摸出2个球，若摸出的“两个都是红球”出现3次获得200分，若摸出“两个都是红球”出现1次或2次获得20分，若摸出“两个都是红球”出现0次则扣除10分（即获得分）．

    （1）设每轮游戏中出现“摸出两个都是红球”的次数为，求的分布列；

    （2）玩过这款游戏的许多人发现，若干轮游戏后，与最初的分数相比，分数没有增加反而减少了，请运用概率统计的相关知识分析解释上述现象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】无线电技术在航海中有很广泛的应用，无线电波可以作为各种信息的载体．现有一艘航行中的轮船需要与陆地上的基站进行通信，其连续向基站拍发若干次呼叫信号，每次呼叫信号被基站收到的概率都是0.2，基站收到呼叫信号后立即向轮船拍发回答信号，回答信号一定能被轮船收到．

    （Ⅰ）若要保证基站收到信号的概率大于0.99，求轮船至少要拍发多少次呼叫信号．

    （Ⅱ）设（Ⅰ）中求得的结果为．若轮船第一次拍发呼叫信号后，每隔5秒钟拍发下一次，直到收到回答信号为止，已知该轮船最多拍发次呼叫信号，且无线电信号在轮船与基站之间一个来回需要16秒，设轮船停止拍发时，一共拍发了次呼叫信号，求的数学期望（结果精确到0.01）．

    参考数据：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的长度单位.已知直线l的参数方程为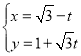（t为参数），曲线C的极坐标方程为ρ＝4sin（θ+）.

    （1）求直线l的普通方程与曲线C的直角坐标方程；

    （2）若直线l与曲线C交于M，N两点，求△MON的面积.

    查看答案和解析>>

    同步练习册答案