
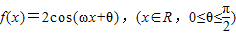 ,g(x)=ex-x2+2ax-1,(x∈R,a为实数),y=f(x)的图象与y轴交于点
,g(x)=ex-x2+2ax-1,(x∈R,a为实数),y=f(x)的图象与y轴交于点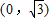 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2.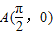 ,点P是函数y=f(x)图象上一点,Q(x,y)是PA的中点,当
,点P是函数y=f(x)图象上一点,Q(x,y)是PA的中点,当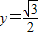 ,
,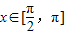 时,求x的值;
时,求x的值; 处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;
处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;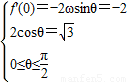 可得:
可得: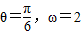

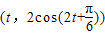 ,已知
,已知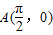
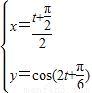 又由
又由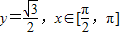 得到t=π或
得到t=π或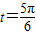
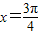 或
或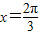
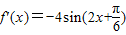 所以曲线f(x)的切线斜率k1∈[-4,4]
所以曲线f(x)的切线斜率k1∈[-4,4]

科目:高中数学 来源:2010年湖南省邵阳市洞口三中高考数学模拟试卷(理科)(解析版) 题型:解答题
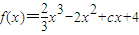 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x),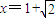 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;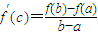 ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.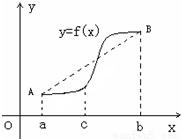
查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省中山市高三学业质量监测数学试卷(理科)(解析版) 题型:解答题
 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x), 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间; ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省中山市高三学业质量监测数学试卷(文科)(解析版) 题型:解答题
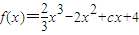 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x), 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间; ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.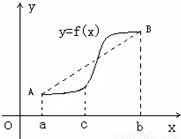
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com