
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 依逆时针次序排列,点
依逆时针次序排列,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(2)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,原点为
,原点为![]() ,椭圆
,椭圆![]() 的动弦
的动弦![]() 过焦点
过焦点![]() 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]() .
.
(1)证明:点![]() 在定直线上;
在定直线上;
(2)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
:![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上不同的三点,并且
上不同的三点,并且![]() 为
为![]() 的重心,试探究
的重心,试探究![]() 的面积是否为定值.若是,求出这个定值;若不是,请说明理由.
的面积是否为定值.若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
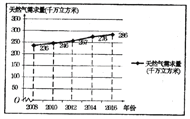
【题目】2017年12月,针对国内天然气供应紧张的问题,某市政府及时安排部署,加气站采取了紧急限气措施,全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况,对该地区某些年份天然气需求量进行了统计,并绘制了相应的折线图.
(Ⅰ)由折线图可以看出,可用线性回归模型拟合年度天然气需示量![]() (单位:千万立方米)与年份
(单位:千万立方米)与年份![]() (单位:年)之间的关系.并且已知
(单位:年)之间的关系.并且已知![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,试确定
,试确定![]() 的值,并预测2018年该地区的天然气需求量;
的值,并预测2018年该地区的天然气需求量;
(Ⅱ)政府部门为节约能源出台了《购置新能源汽车补贴方案》,该方案对新能源汽车的续航里程做出了严格规定,根据续航里程的不同,将补贴金额划分为三类,A类:每车补贴1万元,B类:每车补贴2.5万元,C类:每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计,结果如下表:
类型 |
|
|
|
车辆数目 | 10 | 20 | 30 |
为了制定更合理的补贴方案,政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况,在该出租车公司的60辆车中抽取6辆车作为样本,再从6辆车中抽取2辆车进一步跟踪调查.若抽取的2辆车享受的补贴金额之和记为“![]() ”,求
”,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某班的50名学生进行不记名问卷调查,内容为本周使用手机的时间长,如表:
时间长(小时) |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为![]() 的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为![]() 被认定“不依赖手机”,
被认定“不依赖手机”,![]() 被认定“依赖手机”,根据以上数据完成
被认定“依赖手机”,根据以上数据完成![]() 列联表:
列联表:
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com