
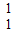 ]ЃЌВЂЧвОиеѓMЖдгІЕФБфЛЛНЋЕуЃЈ-1ЃЌ2ЃЉБфЛЛГЩЃЈ9ЃЌ15ЃЉЃЌЧѓОиеѓMЃЎ
]ЃЌВЂЧвОиеѓMЖдгІЕФБфЛЛНЋЕуЃЈ-1ЃЌ2ЃЉБфЛЛГЩЃЈ9ЃЌ15ЃЉЃЌЧѓОиеѓMЃЎ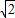 sinЃЈ
sinЃЈ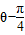 ЃЉЃЌвдМЋЕуЮЊдЕуЃЌМЋжсЮЊxжсЕФе§АыжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊ
ЃЉЃЌвдМЋЕуЮЊдЕуЃЌМЋжсЮЊxжсЕФе§АыжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊ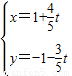 ЃЈtЮЊВЮЪ§ЃЉЃЌЧѓжБЯпlБЛЧњЯпCЫљНиЕУЕФЯвГЄЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЌЧѓжБЯпlБЛЧњЯпCЫљНиЕУЕФЯвГЄЃЎ
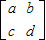 ЃЌдђ
ЃЌдђ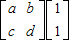 =3
=3 =
= ЃЌ
ЃЌ =
= ЃЌгЩДЫФмЧѓГіMЃЎ
ЃЌгЩДЫФмЧѓГіMЃЎ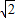 sinЃЈ
sinЃЈ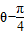 ЃЉЃЌ
ЃЉЃЌ ЗжБ№ЛЏЮЊЦеЭЈЗНГЬЃКx2+y2+2x-2y=0ЃЌ3x+4y+1=0ЃЌгЩДЫФмЧѓГіЯвГЄЃЎ
ЗжБ№ЛЏЮЊЦеЭЈЗНГЬЃКx2+y2+2x-2y=0ЃЌ3x+4y+1=0ЃЌгЩДЫФмЧѓГіЯвГЄЃЎ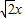 ЃЉ2+ЃЈ
ЃЉ2+ЃЈ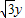 ЃЉ2+z2]•[ЃЈ
ЃЉ2+z2]•[ЃЈ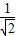 ЃЉ2+ЃЈ
ЃЉ2+ЃЈ ЃЉ2+12]ЃЌЙЪ
ЃЉ2+12]ЃЌЙЪ ЃЌгЩДЫФмЧѓГі2x2+3y2+z2ЕФзюаЁжЕЃЎ
ЃЌгЩДЫФмЧѓГі2x2+3y2+z2ЕФзюаЁжЕЃЎ AЃЎбЁао4-1ЃКЃЈМИКЮжЄУїбЁНВЃЉ
AЃЎбЁао4-1ЃКЃЈМИКЮжЄУїбЁНВЃЉ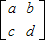 ЃЌдђ
ЃЌдђ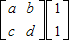 =3
=3 =
= ЃЌ
ЃЌ ЃЎЁЃЈ4ЗжЃЉ
ЃЎЁЃЈ4ЗжЃЉ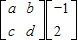 =
= ЃЌЙЪ
ЃЌЙЪ ЃЎЁЃЈ7ЗжЃЉ
ЃЎЁЃЈ7ЗжЃЉ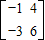 ЃЎ ЁЃЈ10ЗжЃЉ
ЃЎ ЁЃЈ10ЗжЃЉ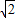 sinЃЈ
sinЃЈ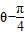 ЃЉЃЌ
ЃЉЃЌ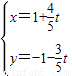 ЗжБ№ЛЏЮЊЦеЭЈЗНГЬЃК
ЗжБ№ЛЏЮЊЦеЭЈЗНГЬЃК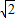 ЃЌ
ЃЌ ЃЌ
ЃЌ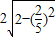 =
= ЃЎЁЃЈ10ЗжЃЉ
ЃЎЁЃЈ10ЗжЃЉ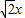 ЃЉ2+ЃЈ
ЃЉ2+ЃЈ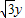 ЃЉ2+z2]•[ЃЈ
ЃЉ2+z2]•[ЃЈ ЃЉ2+ЃЈ
ЃЉ2+ЃЈ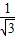 ЃЉ2+12]ЃЌЁЃЈ5ЗжЃЉ
ЃЉ2+12]ЃЌЁЃЈ5ЗжЃЉ ЃЌ
ЃЌ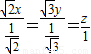 ЃЌ
ЃЌ ЃЌy=
ЃЌy=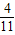 ЃЌz=
ЃЌz=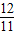 ЪБЃЌ
ЪБЃЌ ЃЎЁЃЈ10ЗжЃЉ
ЃЎЁЃЈ10ЗжЃЉ


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 дкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎЧыдкД№ЬтжНжИЖЈЧјгђФк зїД№ЃЎНтД№гІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ
дкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎЧыдкД№ЬтжНжИЖЈЧјгђФк зїД№ЃЎНтД№гІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 бЁзіЬтдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎ
бЁзіЬтдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎ| 1 |
| 3 |
|
| ІТ |
|
| a |
| a |
| ІТ |
| a |
| 3cos2ІШ+4sin2ІШ |
| (a+b+c)2 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈбЁзіЬтЃЉдкAЃЌBЃЌCЃЌDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎЧыдкД№ЬтПЈжИЖЈЧјгђФкзїД№ЃЌНтД№ЪБгІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ
ЃЈбЁзіЬтЃЉдкAЃЌBЃЌCЃЌDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВМЦ20ЗжЃЎЧыдкД№ЬтПЈжИЖЈЧјгђФкзїД№ЃЌНтД№ЪБгІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ| 3 |
| 3 |
|
| 2 |
| Іа |
| 4 |
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 бЁзіЬтЃКдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВ20ЗжЃЎНтД№гІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ
бЁзіЬтЃКдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзі2ЬтЃЌУПаЁЬт10ЗжЃЌЙВ20ЗжЃЎНтД№гІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЎ
|
|
| 2 |
| Іа |
| 4 |
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 бЁзіЬтЃЈдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзіСНЬтЃЌВЂНЋбЁзїБъМЧгУ2BЧІБЪЭПКкЃЌУПаЁЬт10ЗжЃЌЙВ20ЗжЃЌЧыдкД№ЬтжИЖЈЧјгђФкзїД№ЃЌНтД№ЪБгІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЉЃЎ
бЁзіЬтЃЈдкAЁЂBЁЂCЁЂDЫФаЁЬтжажЛФмбЁзіСНЬтЃЌВЂНЋбЁзїБъМЧгУ2BЧІБЪЭПКкЃЌУПаЁЬт10ЗжЃЌЙВ20ЗжЃЌЧыдкД№ЬтжИЖЈЧјгђФкзїД№ЃЌНтД№ЪБгІаДГіЮФзжЫЕУїЁЂжЄУїЙ§ГЬЛђбнЫуВНжшЃЉЃЎ
|
| Іа |
| 4 |
| ||
| 2 |
| ab |
| bc |
| ca |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com