
【题目】关于x的方程22x﹣(m﹣1)2x+2=0在x∈[0,2]时有唯一解,求m取值范围.
【答案】解:令2x=t,则t∈[1,4], ∴方程t2﹣(m﹣1)t+2=0在[1,4]上有唯一解.
①若△=(m﹣1)2﹣8=0,即m=1±2 ![]() 时,
时,
若m=1+2 ![]() ,则t=
,则t= ![]() ,符合题意,
,符合题意,
若m=1﹣2 ![]() ,则t=﹣
,则t=﹣ ![]() ,不符合题意.
,不符合题意.
②若△=(m﹣1)2﹣8>0,即m<1﹣2 ![]() 或m>1+2
或m>1+2 ![]() 时,
时,
若t=1是方程的解,由根与系数的关系可知t=2也是方程的解,与方程在[1,4]上有唯一解矛盾;
若t=4是方程的解,由根与系数的关系可知t= ![]() 也是方程的解,符合题意;
也是方程的解,符合题意;
此时m﹣1=4+ ![]() ,∴m=
,∴m= ![]() .
.
若方程的解在(1,4)上,根据零点的存在性定理可知(4﹣m)(22﹣4m)<0,
解得4<m< ![]() .
.
综上,m的取值范围是(4, ![]() ]∪{1+2
]∪{1+2 ![]() }
}
【解析】令2x=t,在方程t2﹣(m﹣1)t+2=0在[1,4]上有唯一解,对判别式和区间端点值进行讨论,利用二次函数的性质和零点的存在性定理得出a的范围.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】若直线l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0的四个交点把圆C分成的四条弧长相等,则m=( )
A.0或1
B.0或﹣1
C.1或﹣1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,
, ![]() .①求数列
.①求数列![]() 的通项公式;②是否存在正整数
的通项公式;②是否存在正整数![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin4x+2cos4x+cos22x﹣3.
(1)求函数f(x)的最小正周期.
(2)求函数f(x)在闭区间[ ![]() ]上的最小值并求当f(x)取最小值时,x的取值集合.
]上的最小值并求当f(x)取最小值时,x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x ![]() )(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣
)(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣ ![]() );
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点 ![]() 对称;
对称;
④y=f(x)的图象关于直线x=﹣ ![]() 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年”的人数之比为9: 11.
(1)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
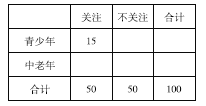
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“国际教育信息化大会”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:参考公式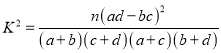 ,其中
,其中![]() .
.
临界值表:
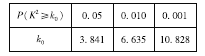
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,两个焦点分别为
,两个焦点分别为![]() ,
, ![]() ,四边形
,四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍.
的面积的2倍.
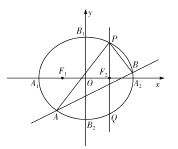
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若直线
两侧的两点.若直线![]() 过点
过点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠CPB=α,∠DPA=β. (Ⅰ)当 ![]() 最小时,求tan∠DPC的值;
最小时,求tan∠DPC的值;
(Ⅱ)当∠DPC=β时,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com