
【题目】如图,某小区中央广场由两部分组成,一部分是边长为![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 为直径的半圆,其圆心为
为直径的半圆,其圆心为![]() .规划修建的
.规划修建的![]() 条直道
条直道![]() ,
, ![]() ,
, ![]() 将广场分割为
将广场分割为![]() 个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点
个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点![]() 在半圆弧上,
在半圆弧上, ![]() 分别与
分别与![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() .(道路宽度忽略不计)
.(道路宽度忽略不计)
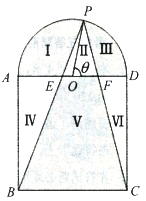
(1)若![]() 经过圆心,求点
经过圆心,求点![]() 到
到![]() 的距离;
的距离;
(2)设![]() ,
, ![]() .
.
①试用![]() 表示
表示![]() 的长度;
的长度;
②当![]() 为何值时,绿化区域面积之和最大.
为何值时,绿化区域面积之和最大.
【答案】(1)![]() (2)①最小值为
(2)①最小值为![]() ②当
②当![]() 时,绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大
时,绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大
【解析】试题分析:(1)先建立直角坐标系,联立直线OB方程与圆方程解得P点纵坐标,即得点![]() 到
到![]() 的距离;(2)①先求点
的距离;(2)①先求点![]() 到
到![]() 的距离为
的距离为![]() ,再根据三角形相似得
,再根据三角形相似得![]() 的长度;②根据三角形面积公式求三个三角形面积,再用总面积相减得绿化区域面积,最后利用导数求函数最值
的长度;②根据三角形面积公式求三个三角形面积,再用总面积相减得绿化区域面积,最后利用导数求函数最值
试题解析:以![]() 所在直线为
所在直线为![]() 轴,以线段
轴,以线段![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)直线![]() 的方程为
的方程为![]() ,
,
半圆![]() 的方程为
的方程为![]()
![]() ,
,
由![]() 得
得![]() .
.
所以,点![]() 到
到![]() 的距离为
的距离为![]() .
.
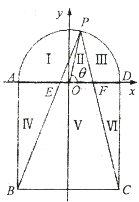
(2)①由题意,得![]() .
.
直线![]() 的方程为
的方程为
![]() ,
,
令![]() ,得
,得
![]()
![]() .
.
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]()
![]() .
.
所以, ![]() 的长度为
的长度为
![]()
![]() ,
, ![]() .
.
②区域Ⅳ、Ⅵ的面积之和为
![]()
![]() ,
,
区域Ⅱ的面积为
![]()
![]()
![]() ,
,
所以![]()
![]() .
.
设![]() ,则
,则![]() ,
,
![]() .
.
![]()
![]()
![]() .
.
当且仅当![]() ,即
,即![]() 时“
时“![]() ”成立.
”成立.
所以,休闲区域Ⅱ、Ⅳ、Ⅵ的面积![]() 的最小值为
的最小值为![]() .
.
答:当![]() 时,绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大.
时,绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.

(1)若![]() ,
,![]() 在
在![]() 上,四面体
上,四面体![]() 是否为鳖臑,若是,写出其每个面的直角:若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角:若不是,请说明理由;
(2)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面半径为![]() ,母线长为
,母线长为![]() 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形![]() ,线段
,线段![]() 上的两动点
上的两动点![]() ,
, ![]() 满足
满足![]() .点
.点![]() 在底面圆
在底面圆![]() 上,且
上,且![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱锥![]() 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-x2)ex-1.
(1)求函数f(x)的单调区间;
(2)若对任意x≥1,都有f(x)-mx-1+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的函数,f′(x)是f(x)的导函数,且满足f′(x)+f(x)<0,设g(x)=exf(x),若不等式g(1+t2)<g(mt)对于任意的实数t恒成立,则实数m的取值范围是( )
A. (﹣∞,0)∪(4,+∞) B. (0,1)
C. (﹣∞,﹣2)∪(2,+∞) D. (﹣2,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,则
,则![]()
C. 若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点, ![]() 为椭圆上异于
为椭圆上异于![]() 的点.
的点.
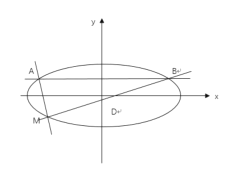
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过
过![]() 点,求圆
点,求圆![]() 的标准方程;
的标准方程;
(3)设直线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一次骰子,将得到的点数分别记为![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com