
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
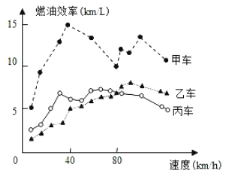
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
科目:高中数学 来源: 题型:
【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
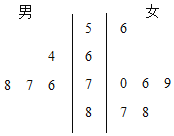
(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA,OB是两条互相垂直的笔直公路,半径OA=2km的扇形AOB是某地的一名胜古迹区域.当地政府为了缓解该古迹周围的交通压力,欲在圆弧AB上新增一个入口P(点P不与A,B重合),并新建两条都与圆弧AB相切的笔直公路MB,MN,切点分别是B,P.当新建的两条公路总长最小时,投资费用最低.设∠POA=![]() ,公路MB,MN的总长为
,公路MB,MN的总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)当![]() 为何值时,投资费用最低?并求出
为何值时,投资费用最低?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
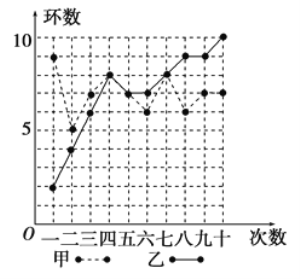
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.存在每个面都是直角三角形的四面体
B.每个面都是三角形的几何体是三棱锥
C.圆台上、下底面圆周上各取一点的连线是母线
D.用一个平面截圆锥,截面与底面间的部分是圆台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接旅游旺季的到来,辽阳汤河风景区内供游客住宿的某宾馆,工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,现每年各个月份来宾馆入住的游客人数会呈现周期性的变化,并且有以下规律:
①每年相同的月份,入住宾馆的游客人数基本相同;
②入住宾馆的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住宾馆的游客约为100人,随后逐月增加直到8月份达到最多.
(1)若一年中入住宾馆的游客人数与月份之间的关系为![]() ,
,![]() 且
且![]() .试求出函数
.试求出函数![]() 的解析式;
的解析式;
(2)请问哪几个月份要准备不少于400份的食物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com