
 与年份
与年份 的统计数据如下表:
的统计数据如下表:年份 | 2004 | 2005 | 2006 | 2007 |
恩格尔系数 (%) (%) | 47 | 45.5 | 43.5 | 41 |
 与
与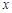 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为 ,据此模型可预测2013年该地区的恩格尔系数(%)为 .
,据此模型可预测2013年该地区的恩格尔系数(%)为 . 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:不详 题型:解答题
| 施化肥量x | 15 | 20 | 25 | 30 |
| 水稻产量y | 330 | 345 | 365 | 405 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
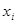 (
(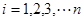 ),如果将它们改变为
),如果将它们改变为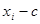 (
(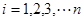 ),其中
),其中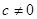 ,下列结论正确的是( )
,下列结论正确的是( )| A.平均数与方差均不变 | B.平均数变了,而方差保持不变 |
| C.平均数不变,而方差变了 | D.平均数与方差均发生了变化 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 商店名称 | A | B | C | D | E |
销售额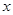 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额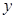 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
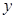 关于销售额
关于销售额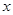 的回归直线方程;
的回归直线方程;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.x;和y正相关 |
| B.y和y的相关系数为直线I的斜率 |
| C.x和y的相关系数在-1到O之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
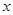 和所支出的维修费用
和所支出的维修费用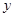 (万元)统计数据如下:
(万元)统计数据如下:| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
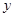 对
对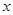 呈线性相关关系.求:
呈线性相关关系.求: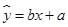 的回归系数;
的回归系数;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 ="x" B.
="x" B. ="0.8x+2.05"
="0.8x+2.05"  =0.7x+1.05 D.
=0.7x+1.05 D.  =0.6x+0.95
=0.6x+0.95 =
= ,
, =
= -
-
 ,
, =
= x+
x+
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

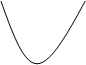









 (1) (2) (3) (4)
(1) (2) (3) (4)| A.(1)(2) | B.(1)(3) | C.(2)(4) | D.(2)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com