练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设，其中，为个互不相同的有限集合，满足对任意、，均有.若（表示有限集合的元素个数），证明：存在，使得属于中的至少个集合.

    【答案】见解析

    【解析】

    不妨设.设在中与不相交的集合有个，重新记为；

    设包含的集合有个，重新记为.先证明，再证明.再证明包含的集合个数至少为.

    不妨设.

    设在中与不相交的集合有个，重新记为；

    设包含的集合有个，重新记为.

    由已知条件，得，即.

    于是，得到一个映射，.

    显然，为单射.从而，.

    设.

    在中除去，后，在剩下的个集合中，设包含的集合有个，由于剩下的个集合中，设包含的集合有个，由于剩下的个集合中每个集合与的交非空，即包含某个，从而，

    . ①

    不妨设.

    则由式①知，即在剩下的个集合中，包含的集合至少有个.

    又由于，故均包含.

    因此，包含的集合个数至少为

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了解某冷饮店的经营状况，随机记录了该店月的月营业额（单位：万元）与月份的数据，如下表：

    （1）求关于的回归直线方程；

    （2）若在这样本点中任取两点，求恰有一点在回归直线上的概率.

    附：回归直线方程中，

    ，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系，随机抽查了100名学生，得到某次期末考试的成绩数据如表1至表3，根据表中数据可知该校学生语文、数学、英语这三门学科中（ ）

    表1

    表2

    表3

    语文

    性别

    不及格

    及格

    总计

    数学

    性别

    不及格

    及格

    总计

    英语

    性别

    不及格

    及格

    总计

    男

    14

    36

    50

    男

    10

    40

    50

    男

    25

    25

    50

    女

    16

    34

    50

    女

    20

    30

    50

    女

    5

    45

    50

    总计

    30

    70

    100

    总计

    30

    70

    100

    总计

    30

    70

    100

    A.语文成绩与性别有关联性的可能性最大，数学成绩与性别有关联性的可能性最小

    B.数学成绩与性别有关联性的可能性最大，语文成绩与性别有关联性的可能性最小

    C.英语成绩与性别有关联性的可能性最大，语文成绩与性别有关联性的可能性最小

    D.英语成绩与性别有关联性的可能性最大，数学成绩与性别有关联性的可能性最小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE，H是直角项点)来处理污水．管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上．已知AB＝20米，AD＝米，记∠BHE＝．

    （1）试将污水净化管道的长度L表示为的函数，并写出定义域；

    （2）当取何值时，污水净化效果最好？并求出此时管道的长度L．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

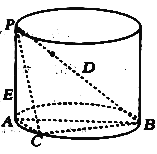
    【题目】如图，是圆柱的直径，是圆柱的母线，，，点是圆柱底面圆周上的点.

    （1）求三棱锥体积的最大值；

    （2）若，是线段上靠近点的三等分点，点是线段上的动点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，为的中点，是线段上的一点.

    （1）若为的中点，求证：平面平面；

    （2）当点在什么位置时，平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）设：实数x满足|x﹣m|＜2，设：实数x满足＞1；若￢p是￢q的必要不充分条件，求实数m的取值范围

    （2）已知p：函数f（x）＝ln（x2﹣ax+3）的定义城为R，已知q：已知且，指数函数g（x）＝（a﹣1）x在实数域内为减函数；若￢p∨q为假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求的单调区间；

    （2）若对于任意，都有，求的取值范围.

    查看答案和解析>>

    同步练习册答案