解:
(Ⅰ)依题意可画图如下:

(Ⅱ)当z=0时,有直线l
1:2x+y=0和直线l
2:2x-y=0,并分别在上图表示出来,
当直线2x+y=0向下平移并过B点的时候,目标函数z=2x+y有最小值,此时最优解就是B点,解方程组

得点B的坐标是:B(-2,3),
因此,目标函数z=2x+y的最小值是:z=2×(-2)+3=-1
同理可得,当直线向2x-y=0向下平移并过C点的时候,目标函数z=2x-y有最大值,此时最优解就是C点,解方程组

得点C的坐标是:C(3,-2),
因此目标函数z=2x-y的最大值是:z=2×3-(-2)=8
分析:(I)先画出可行域的边界,即三个直线方程对应的直线,再利用一元二次不等式表示平面区域的规律,确定可行域,画成阴影即可;
(II)将目标函数的函数值看做目标函数对应直线的纵截距,平移目标函数,数形结合找到最优解即可
点评:本题考查了线性规划的方法和思想,一元二次不等式表示平面区域的规律和区域的画法,利用可行域数形结合求目标函数最值的方法

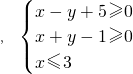 ,请完成下列问题.
,请完成下列问题.
 得点B的坐标是:B(-2,3),
得点B的坐标是:B(-2,3), 得点C的坐标是:C(3,-2),
得点C的坐标是:C(3,-2),

 阅读快车系列答案
阅读快车系列答案