
【题目】已知点A,B的坐标分别是(![]() ,0),(
,0),(![]() ,0),动点M(x,y)满足直线AM和BM的斜率之积为﹣3,记M的轨迹为曲线E.
,0),动点M(x,y)满足直线AM和BM的斜率之积为﹣3,记M的轨迹为曲线E.
(1)求曲线E的方程;
(2)直线y=kx+m与曲线E相交于P,Q两点,若曲线E上存在点R,使得四边形OPRQ为平行四边形(其中O为坐标原点),求m的取值范围.
【答案】(1)![]() ,(y≠0);(2)(﹣∞,
,(y≠0);(2)(﹣∞,![]() ]∪[
]∪[![]() ,+∞).
,+∞).
【解析】
(1)根据题意得kAMkBM![]()
![]() 3,(y≠0),化简可得曲线E的方程.
3,(y≠0),化简可得曲线E的方程.
(2))设P(x1,y1),Q(x2,y2),联立直线与曲线E的方程,得关于x的一元二次方程,结合韦达定理得x1+x2,y1+y2,△>0①,根据题意得PQ的中点也是OR的中点,得R点的坐标,再代入曲线E的方程,得2m2=k2+3②,将②代入①得m的取值范围.
解:(1)kAMkBM![]()
![]() 3,(y≠0)
3,(y≠0)
化简得曲线E的方程:![]() .(y≠0)
.(y≠0)
(2)设P(x1,y1),Q(x2,y2)
联立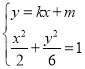 ,得(3+k2)x2+2kmx+m2﹣6=0,
,得(3+k2)x2+2kmx+m2﹣6=0,
x1+x2![]() ,y1+y2=k(x1+x2)+2m
,y1+y2=k(x1+x2)+2m![]() ,
,
△=(2km)2﹣4×(3+k2)(m2﹣6)=﹣12m2+24k2+72>0,即﹣m2+2k2+6>0,①
若四边形OPRQ为平行四边形,则PQ的中点也是OR的中点,
所以R点的坐标为(![]() ,
,![]() ),
),
又点R在曲线E上得, 化简得2m2=k2+3②
化简得2m2=k2+3②
将②代入①得,m2>0,所以m≠0,由②得2m2≥3,所以m![]() 或m
或m![]()
所以m的取值范围为(﹣∞,![]() ]∪[
]∪[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系![]() 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),射线
),射线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 交于(不包括极点
交于(不包括极点![]() )三点
)三点![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,
时,![]() ,
,![]() 两点在曲线
两点在曲线![]() 上,求
上,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等比数列,其前
为等比数列,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.![]() 为等差数列,其前
为等差数列,其前![]() 项和为
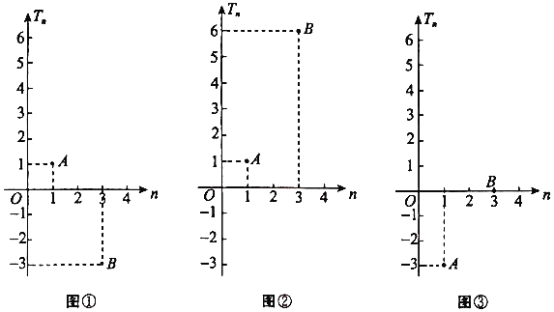
项和为![]() ,如图_____,
,如图_____,![]() 的图象经过
的图象经过![]() 两个点.
两个点.
(Ⅰ)求![]() ;
;
(Ⅱ)若存在正整数![]() ,使得
,使得![]() ,求
,求![]() 的最小值.从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答.
的最小值.从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]()
![]() 的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题
的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题![]() 随机变量
随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .现给出四个命题:①
.现给出四个命题:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中真命题的是( )
,其中真命题的是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2019年9月到2020年2月这半年中,某个关键词的搜索指数变化的走势图.
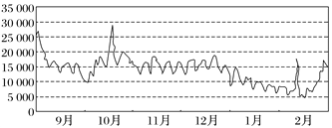
根据该走势图,下列结论不正确的是( ).
A.这半年中,网民对该关键词相关的信息关注度与时间具有比较明显的线性相关性
B.2019年10月网民对该关键词的搜索指数变化的走势图具有较好的对称性,与正态曲线相近,故当月搜索指数的平均值约为29000
C.从网民对该关键词的搜索指数来看,2019年10月的方差小于11月的方差
D.从网民对该关键词的搜索指数来看,2019年12月的平均值大于2020年1月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
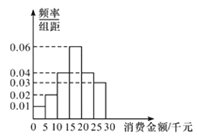
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
80 | 40 | 16 | 24 | |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: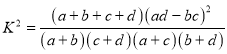
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为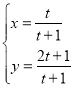 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com