练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c.已知a2+c2＝b2ac.

    （1）求cosB及tan2B的值；

    （2）若b＝3，A，求c的值.

    【答案】（1）cosB，tan2B（2）2

    【解析】

    （1）由已知利用余弦定理可得cosB，利用同角三角函数基本关系式可求sinB，利用二倍角公式可求sin2B，cos2B，进而根据同角三角函数基本关系式可求tan2B的值.

    （2）由已知利用两角和的正弦函数公式可求sinC的值，进而由正弦定理可得c的值.

    （1）∵a2+c2＝b2ac，

    ∴由余弦定理可得：cosB，

    ∴sinB，

    ∴sin2B＝2sinBcosB，cos2B＝2cos2B﹣1，

    ∴tan2B；

    （2）∵sinC＝sin[π﹣（A+B）]＝sin（A+B）＝sin（B）＝sinBcoscosBsin.

    ∴由正弦定理，可得c2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设，，，给出以下四种排序：①M，N，T；②M，T，N；③N，T，M；④T，N，M．从中任选一个，补充在下面的问题中，解答相应的问题．

    已知等比数列中的各项都为正数，，且__________依次成等差数列．

    （Ⅰ）求的通项公式；

    （Ⅱ）设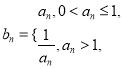数列的前n项和为，求满足的最小正整数n．

    注：若选择多种排序分别解答，按第一个解答计分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c为正实数，且满足a+b+c＝1.证明：

    （1）|a|+|b+c﹣1|；

    （2）（a3+b3+c3）（）≥3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】携号转网，也称作号码携带、移机不改号，即无需改变自己的手机号码，就能转换运营商，并享受其提供的各种服务．2019年11月27日，工信部宣布携号转网在全国范围正式启动．某运营商为提质量保客户，从运营系统中选出300名客户，对业务水平和服务水平的评价进行统计，其中业务水平的满意率为，服务水平的满意率为，对业务水平和服务水平都满意的客户有180人．

    （Ⅰ）完成下面列联表，并分析是否有的把握认为业务水平与服务水平有关；

    对服务水平满意人数

    对服务水平不满意人数

    合计

    对业务水平满意人数

    对业务水平不满意人数

    合计

    （Ⅱ）为进一步提高服务质量，在选出的对服务水平不满意的客户中，抽取2名征求改进意见，用表示对业务水平不满意的人数，求的分布列与期望；

    （Ⅲ）若用频率代替概率，假定在业务服务协议终止时，对业务水平和服务水平两项都满意的客户流失率为，只对其中一项不满意的客户流失率为，对两项都不满意的客户流失率为，从该运营系统中任选4名客户，则在业务服务协议终止时至少有2名客户流失的概率为多少？

    附：，．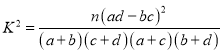

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且，数列是公差为0的等差数列，且满足，是和的等比数列.

    （1）求数列和的通项公式；

    （2）求；

    （3）设数列的通项公式，求；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在贯彻精准扶贫政策的过程中，某单位在某市定点帮扶甲、乙两村各户贫困户，工作组对这户村民的年收入、劳动能力、子女受教育等情况等进行调查，并把调查结果转换为贫困指标，再将指标分成、、、、五组，得到如下图所示的频率分布直方图．若规定，则认定该户为“绝对贫困户”，否则认定该户为“相对贫困户”，且当时，认定该户为“低收入户”，当时，认定该户为“亟待帮助户”．已知此次调查中甲村的“绝对贫困户”占甲村贫困户的．

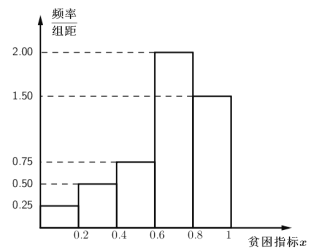
    （1）完成下列列联表，并判断是否有的把握认为“绝对贫困户”数与村落有关；

    （2）某干部决定在这两村贫困指标在、内的贫困户中，利用分层抽样抽取户，现从这户中再随机选取户进行帮扶，求所选户中至少有一户是“亟待帮助户”的概率．

    甲村

    乙村

    总计

    绝对贫困户

    相对贫困户

    总计

    附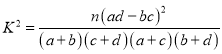：，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年3月12日，国务院新闻办公室发布会重点介绍了改革开放40年，特别是党的十八大以来我国脱贫攻坚、精准扶贫取得的显著成绩，这些成绩为全面脱贫初步建成小康社会奠定了坚实的基础．下图是统计局公布的2010年～2019年年底的贫困人口和贫困发生率统计表．则下面结论正确的是（ ）

    （年底贫困人口的线性回归方程为(其中年份-2019)，贫困发生率的线性回归方程为(其中年份-2009)）

    A.2010年～2019年十年间脱贫人口逐年减少，贫困发生率逐年下降

    B.2012年~2019年连续八年每年减贫超过1000万，且2019年贫困发生率最低

    C.2010年～2019年十年间超过1.65亿人脱贫，其中2015年贫困发生率低于6％

    D.根据图中趋势线可以预测，到2020年底我国将实现全面脱贫

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，四点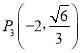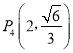，，，中恰有三个点在椭圆C上，左、右焦点分别为F1、F2．

    （1）求椭圆C的方程；

    （2）过左焦点F1且不平行坐标轴的直线l交椭圆于P、Q两点，若PQ的中点为N，O为原点，直线ON交直线x＝﹣3于点M，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为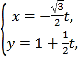（为参数），以原点为极点， 轴正半轴为极轴建立极坐标系，曲线的方程为，定点，点是曲线上的动点， 为的中点.

    （1）求点的轨迹的直角坐标方程；

    （2）已知直线与轴的交点为，与曲线的交点为，若的中点为，求的长.

    查看答案和解析>>

    同步练习册答案