
| A. | $\frac{64}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{56}{3}$ | D. | $\frac{38}{3}$ |
分析 联立y=x-4与曲线y=$\sqrt{2x}$,解得$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$.直线y=x-4与坐标轴的交点分别为B(4,0),C(0,-4).可得由直线y=x-4,利用微积分基本定理可得:直线y=x-4,曲线y=$\sqrt{2x}$及x轴所围成的图形的面积S=${∫}_{0}^{8}(\sqrt{2x}-x+4)dx$-S△OBC.
解答 解:如图所示,
联立y=x-4与曲线y=$\sqrt{2x}$,解得$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$.
直线y=x-4与坐标轴的交点分别为B(4,0),C(0,-4).
∴由直线y=x-4,曲线y=$\sqrt{2x}$及x轴所围成的图形的面积
S=${∫}_{0}^{8}(\sqrt{2x}-x+4)dx$-S△OBC
=($\frac{2\sqrt{2}}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{2}$x2+4x)${|}_{0}^{8}$-$\frac{1}{2}$×4×4
=$\frac{40}{3}$.
故选B.
点评 本题考查了微积分基本定理的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
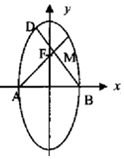 已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.
已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{π}{3}]$ | B. | $(0,\frac{π}{6}]$ | C. | $[\frac{π}{3},π)$ | D. | $[\frac{π}{6},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com