
����Ŀ���ס��ҡ��������ĸ�����ͬʱ��ijһ�������ͬһ�������˶�����·�� ![]()
![]() ����ʱ��
����ʱ�� ![]() �ĺ�����ϵʽ�ֱ�Ϊ
�ĺ�����ϵʽ�ֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �������½��ۣ�
�������½��ۣ�
�ٵ� ![]() ʱ����������ǰ�棻
ʱ����������ǰ�棻
�ڵ� ![]() ʱ����������ǰ�棻
ʱ����������ǰ�棻
�۵� ![]() ʱ����������ǰ�棬��
ʱ����������ǰ�棬�� ![]() ʱ������������棻
ʱ������������棻
�ܱ�������������ǰ�棬Ҳ��������������棻
���������һֱ�˶���ȥ������������ǰ����Ǽף�
���У���ȷ���۵����Ϊ������ȷ���۵���Ŷ����ϣ��������������÷֣���
���𰸡��ۢܢ�
��������·�� ![]() ����ʱ��
����ʱ�� ![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
������Ӧ�ĺ���ģ�ͷֱ���ָ���ͺ��������κ�����һ�κ������Ͷ����ͺ���ģ�ͣ�
�� ![]() ʱ��
ʱ�� ![]() ,������ٲ���ȷ��
,������ٲ���ȷ��
�� ![]() ʱ��
ʱ�� ![]() ��������ڲ���ȷ��
��������ڲ���ȷ��
�����ͺ����ı仯���ȿ�������� ![]() ʱ���ס��ҡ��������ĸ������غϣ��Ӷ���֪��
ʱ���ס��ҡ��������ĸ������غϣ��Ӷ���֪�� ![]() ʱ����������ǰ�棬��
ʱ����������ǰ�棬�� ![]() ʱ������������棬�������ȷ��ָ���ͺ����仯��������죬���˶���ʱ���㹻��ʱ����ǰ�������һ���ǰ���ָ���ͺ����˶������壬��һ���Ǽ����壬���������ȷ��
ʱ������������棬�������ȷ��ָ���ͺ����仯��������죬���˶���ʱ���㹻��ʱ����ǰ�������һ���ǰ���ָ���ͺ����˶������壬��һ���Ǽ����壬���������ȷ��
��϶����ͺ�ָ���ͺ�����ͼ��仯�������֪��������������ǰ�棬Ҳ��������������棬�������ȷ��
������������ָ���ͺ��������κ�����һ�κ������Ͷ����ͺ���ģ�ʹ�����ֵ���������ɡ�


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ ![]() ��ͼ���������ĸ�ƽ�Ʊ任�����Եõ�����y=5sin2x��ͼ�� ��
��ͼ���������ĸ�ƽ�Ʊ任�����Եõ�����y=5sin2x��ͼ�� ��
A.����ƽ�� ![]()
B.����ƽ�� ![]()
C.����ƽ�� ![]()
D.����ƽ�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��0��b��0�������㣨��
=1��a��0��b��0�������㣨�� ![]() ��
�� ![]() ������������Ϊ
������������Ϊ ![]() ��
��
��1������ԲC�ķ��̣�
��2��������ԲC����F���������ഹֱ�Ķ���AB��CD������A��B��C��D�ĵ㹹�ɵ��ı��ε����ΪS����S�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����[��3��0���ȣ�0��3]�ϵ��溯������x�ʣ�0��3]ʱ��f��x����ͼ����ͼ��ʾ����ô���㲻��ʽf��x����2x��1 ��x��ȡֵ��Χ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������������Ϊ ![]() Ԫ����Ʒ��ÿ��
Ԫ����Ʒ��ÿ�� ![]() Ԫ���ۣ���ÿ�������
Ԫ���ۣ���ÿ������� ![]() ������������������ۼۣ����ٽ������İ취����������֪������Ʒÿ�����ۼ����
������������������ۼۣ����ٽ������İ취����������֪������Ʒÿ�����ۼ���� ![]() Ԫ����������Ҫ����
Ԫ����������Ҫ���� ![]() �������ʹ��ÿ���������������ô��Ӧ��ÿ�������ۼ۶�Ϊ�� ��
�������ʹ��ÿ���������������ô��Ӧ��ÿ�������ۼ۶�Ϊ�� ��
A.![]() Ԫ
Ԫ
B.![]() Ԫ
Ԫ
C.![]() Ԫ
Ԫ
D.![]() Ԫ
Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ������A1B1C1��ABC����BCA=90�㣬��D1 �� F1�ֱ���A1B1 �� A1C1���е㣬BC=CA=CC1 �� ��BD1��AF1���ɽǵ�����ֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�Ƿ���2(lg x)2��lg x6��3��0������ʵ������lg(ab)��(logab��logba)��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABCD��A1B1C1D1�У���֪EΪ��CC1�ϵĶ��㣮 
��1����֤��A1E��BD��
��2���Ƿ����������E�㣬ʹ��ƽ��A1BD��ƽ��EBD�������ڣ����ҳ�������E�㣻�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽��У����ѧ���γ̵Ľ�ѧЧ������֯ȫ�и�ѧУ�߶��꼶ȫ��ѧ���μ��˹�ѧ֪ʶˮƽ���ԣ����Գɼ��Ӹߵ������η�ΪA��B��C��D�ĸ��ȼ�����������˼ס�������ѧУ��60��ѧ���ijɼ����õ����µķֲ�ͼ��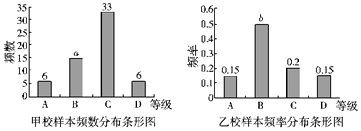
������ȷ��ͼ�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
���������ȼ�A��B��C��D���ΰ��� ![]() �֡�80�֡�60�֡�50��ת���ɷ������Էֱ������Уѧ����ѧ�ɼ��ľ�ֵ��
�֡�80�֡�60�֡�50��ת���ɷ������Էֱ������Уѧ����ѧ�ɼ��ľ�ֵ��
������У���A�ȼ���ͬѧ�а�������ȡ5�˲μӼ�ѵ����ѵ�����ڳɼ��൱�������������ѡ2�˴������вμ�ʡ������������������ͬһѧУ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com