
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为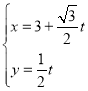 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点、以
为极点、以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求线段![]() 的中点
的中点![]() 的直角坐标;
的直角坐标;
(2)设点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)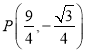 (2)
(2)![]()
【解析】
(1)将曲线![]() 的极坐标方程化为直角坐标方程,再将直线
的极坐标方程化为直角坐标方程,再将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,设
的直角坐标方程,设![]() 、
、![]() 的参数分别为
的参数分别为![]() 、
、![]() ,利用韦达定理求出线段
,利用韦达定理求出线段![]() 中点
中点![]() 对应的参数,代入直线
对应的参数,代入直线![]() 的参数方程可求得点
的参数方程可求得点![]() 的直角坐标;
的直角坐标;
(2)利用弦长公式求得![]() ,求出圆心到直线
,求出圆心到直线![]() 的距离,由此可求得圆
的距离,由此可求得圆![]() 上的点
上的点![]() 到直线
到直线![]() 距离的最大值,利用三角形的面积公式可求得
距离的最大值,利用三角形的面积公式可求得![]() 面积的最大值.
面积的最大值.
(1)将曲线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,化为直角坐标方程得
,化为直角坐标方程得![]() ,
,
将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程得:
的直角坐标方程得: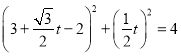 ,化简得
,化简得![]() ,
,
设![]() 、
、![]() 的参数分别为
的参数分别为![]() 、
、![]() ,由韦达定理得:
,由韦达定理得:![]() ,于是
,于是![]() .
.
设![]() ,则
,则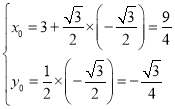 ,
,
故点![]() 的直角坐标为
的直角坐标为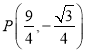 ;
;
(2)由(1)知:![]() ,
,![]() ,
,
所以,![]() ,
,
又直线![]() 的普通方程为
的普通方程为![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为
的距离为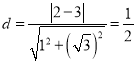 ,圆的半径
,圆的半径![]() .
.
所以,点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
因此,![]() 面积的最大值为:
面积的最大值为:![]() .
.


科目:高中数学 来源: 题型:
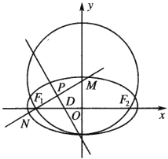
【题目】圆![]() 过椭圆
过椭圆![]() 的下顶点及左、右焦点
的下顶点及左、右焦点![]() ,
,![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() 且垂足为点
且垂足为点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:当直线![]() 斜率变化时
斜率变化时![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点与抛物线
右焦点与抛物线![]() 的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线
的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程
(2)若直线![]() 与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,
与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,![]() ,
,![]() 的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知的有中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重的疾病,新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株,某小区为进一步做好新型冠状病毒肺炎疫情知识的教育,在小区内开展“新型冠状病毒防疫安全公益课”在线学习,在此之后组织了“新型冠状病毒防疫安全知识竞赛”在线活动.已知进入决赛的分别是甲、乙、丙、丁四位业主,决赛后四位业主相应的名次为第1,2,3,4名,该小区为了提高业主们的参与度和重视度,邀请小区内的所有业主在比赛结束前对四位业主的名次进行预测,若预测完全正确将会获得礼品,现用a,b,c,d表示某业主对甲、乙、丙、丁四位业主的名次做出一种等可能的预测排列,记X=|a﹣1|+|b﹣2|+|c﹣3|+|d﹣4|.
(1)求该业主获得礼品的概率;
(2)求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
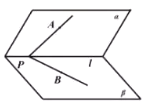
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1,E,F分别是棱CC1,AB的中点.
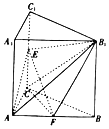
(1)证明:CF∥平面AEB1.
(2)若AC=BC=AA1=4,∠ACB=90°,求三棱锥B1﹣ECF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,且过点
的焦距为2,且过点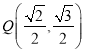 .
.
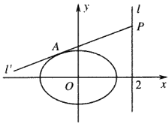
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为直线
为直线![]() 上的一动点,过点
上的一动点,过点![]() 作直线
作直线![]() 与椭圆相切于点
与椭圆相切于点![]() ,若
,若![]() 的面积
的面积![]() 为
为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在CD上,且
,点E在CD上,且![]() ,将
,将![]() 沿AE折起,使得平面
沿AE折起,使得平面![]() 平面ABCE(如图2),G为AE中点.
平面ABCE(如图2),G为AE中点.

(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)在线段BD上是否存在点P,使得![]() 平面ADE?若存在,求
平面ADE?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,.
,.![]() .,
.,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的前n项和为
…的前n项和为![]() ,正整数
,正整数![]() ,
,![]() 满足:①
满足:①![]() ,②
,②![]() 是满足不等式
是满足不等式![]() 的最小正整数,则
的最小正整数,则![]() ( )
( )
A.6182B.6183C.6184D.6185
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com