

 .(12分)
.(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
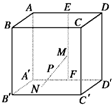 如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (1)已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′如图所示,其中A′D′=2,B′C′=4,A′B′=1,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积.
(1)已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′如图所示,其中A′D′=2,B′C′=4,A′B′=1,求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
 | |||
 | |||
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北武汉市高三2月调研测试理科数学试卷(解析版) 题型:选择题
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二上学期期中考试数学试卷(解析版) 题型:选择题
(文)如图,在棱长为4的正方体ABCD—A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′?上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
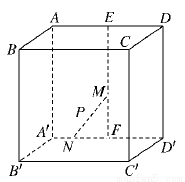
A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com