
 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 的分布列与数学期望。
的分布列与数学期望。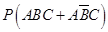
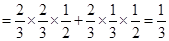
 的分布列
的分布列 | 0 | 1 | 2 | 3 |
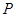 |  | 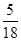 | 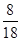 | 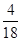 |
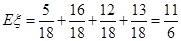
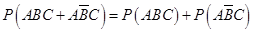 ,然后借助于独立事件的乘法公式得到。
,然后借助于独立事件的乘法公式得到。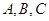 ,则事件“得分不低于8分”表示为
,则事件“得分不低于8分”表示为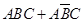 .因为
.因为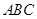 和为互斥事件
和为互斥事件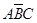 ,且
,且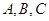 彼此独立,
彼此独立,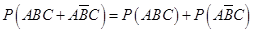
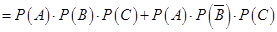
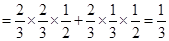 ……………………………5分
……………………………5分 的取值为
的取值为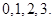
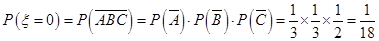 …………………7分
…………………7分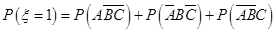
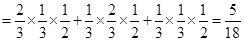

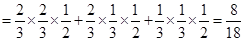
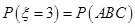
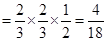
 的分布列
的分布列 | 0 | 1 | 2 | 3 |
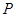 |  | 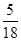 | 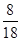 | 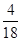 |
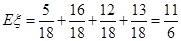


科目:高中数学 来源:不详 题型:解答题
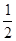 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 到站时刻 | 8∶10 9∶10 | 8∶30 9∶30 | 8∶50 9∶50 |
| 概率 |  |  | 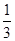 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
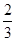 ,乙获胜的概率为
,乙获胜的概率为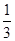 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
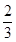 ,被乙小组攻克的概率为
,被乙小组攻克的概率为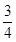 ,
,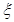 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求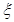 的分布列及数学期望
的分布列及数学期望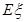 ;
;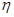 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数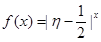 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com