
【题目】已知数列{an}的前n项和是Sn , 且Sn+ ![]() an=1(n∈N*).
an=1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log4(1﹣Sn+1)(n∈N*),Tn= ![]() +
+ ![]() +…+
+…+ ![]() ,求使Tn≥
,求使Tn≥ ![]() 成立的最小的正整数n的值.
成立的最小的正整数n的值.
【答案】
(1)解:当n=1时,a1=S1,由S1+ ![]() a1=1a1=
a1=1a1= ![]() ,
,
当n≥2时,Sn+ ![]() an=1①,Sn﹣1+
an=1①,Sn﹣1+ ![]() an﹣1=1②,
an﹣1=1②,
①﹣②,得 ![]() =0,即an=
=0,即an= ![]() an﹣1,
an﹣1,
∴{an}是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列.
为公比的等比数列.
故an= ![]() =3
=3 ![]() (n∈N*);
(n∈N*);
(2)解:由(1)知1﹣Sn+1= ![]() =
= ![]() ,
,
bn=log4(1﹣Sn+1)= ![]() =﹣(n+1),
=﹣(n+1),
![]() =
= ![]() ,
,
Tn= ![]() +
+ ![]() +…+
+…+ ![]() =(
=( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )=
)= ![]() ,
,
![]() ≥
≥ ![]() 成立的最小的正整数n的值n=2014.
成立的最小的正整数n的值n=2014.
【解析】(1)n=1时,易求a1= ![]() ,当n≥2时,Sn+
,当n≥2时,Sn+ ![]() an=1①,Sn﹣1+
an=1①,Sn﹣1+ ![]() an﹣1=1②,①﹣②可得数列递推式,由此可判断{an}是等比数列,从而可求an . (2)由(1)可求得bn , 利用裂项相消法可求得Tn , 然后可解得不等式Tn≥
an﹣1=1②,①﹣②可得数列递推式,由此可判断{an}是等比数列,从而可求an . (2)由(1)可求得bn , 利用裂项相消法可求得Tn , 然后可解得不等式Tn≥ ![]() 得到答案;
得到答案;
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系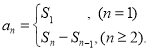 .
.


科目:高中数学 来源: 题型:
【题目】已知n∈N* , 设Sn是单调递减的等比数列{an}的前n项和,a1= ![]() 且S2+a2 , S4+a4 , S3+a3成等差数列.
且S2+a2 , S4+a4 , S3+a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{nan}的前n项和为Tn , 求证:对于任意正整数n, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】虽然吸烟有害健康,但是由于历史以及社会的原因,吸烟也是部分公民交际的重要媒介.世界卫生组织1987年11月建议把每年的4月7日定为世界无烟日,且从1989年开始,世界无烟日改为每年的5月31日.某报社记者专门对吸烟的市民做了戒烟方面的调查,经抽样只有![]() 的烟民表示愿意戒烟,将频率视为概率.
的烟民表示愿意戒烟,将频率视为概率.
(1)从该市吸烟的市民中随机抽取3位,求至少有一位烟民愿意戒烟的概率;
(2)从该市吸烟的市民中随机抽取4位, ![]() 表示愿意戒烟的人数,求
表示愿意戒烟的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 既有一个极小值又有一个极大值,求
既有一个极小值又有一个极大值,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单增函数;若
上的非严格单增函数;若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单减函数.已知:
上的非严格单减函数.已知: ![]() .
.
(1)若函数![]() 为定义在
为定义在![]() 上的非严格单增函数,求实数
上的非严格单增函数,求实数![]() 的取值范围.
的取值范围.
(2)若函数![]() 为定义在
为定义在![]() 上的非严格单减函数,试解不等式
上的非严格单减函数,试解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:函数f(x)= ![]() (a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0,
(a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0, ![]() ],x2﹣a≤0恒成立.
],x2﹣a≤0恒成立.
(1)求命题q真时a的取值范围;
(2)若命题p∧q为假,p∨q为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx(sinx+ ![]() cosx)﹣1(其中x∈R),求:
cosx)﹣1(其中x∈R),求:
(1)函数f(x)的最小正周期;
(2)函数f(x)的单调减区间;
(3)函数f(x)图象的对称轴和对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com