
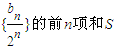 .
.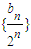 中即可求出其表达式,然后求出其前n项和Sn的表达式,然后利用错位相减法求出
中即可求出其表达式,然后求出其前n项和Sn的表达式,然后利用错位相减法求出 Sn的表达式,即可求出Sn的表达式.
Sn的表达式,即可求出Sn的表达式.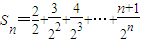 ①
①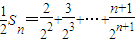 ②
②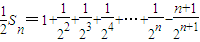 …(13分)
…(13分)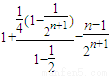 =
=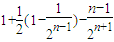
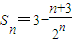 …(16分)
…(16分)

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
| bn | 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)已知由正数组成的两个数列![]() ,如果
,如果![]() 是关于x的方程
是关于x的方程![]() 的两根.
的两根.
(1)求证:![]() 为等差数列;
为等差数列;![]() w w w.k s 5 u.c o m
w w w.k s 5 u.c o m
(2)已知![]() 分别求数列
分别求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| bn |
| 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com