
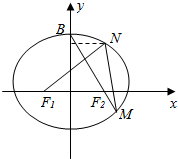
 ��ͼ����֪F1��F2�ֱ�����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬����B�������ǣ�0��b��������BF2���ӳ�����Բ�ڵ�M����M����x��ĶԳƵ�ΪN������F1��N��
��ͼ����֪F1��F2�ֱ�����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬����B�������ǣ�0��b��������BF2���ӳ�����Բ�ڵ�M����M����x��ĶԳƵ�ΪN������F1��N������ ��������Բ�Ķ��壬�������̹�ϵ�������a��b��ֵ�����ɵõ���Բ���̣�
�������C�����꣬����F1C��AB����б��֮��Ĺ�ϵ���ⷽ�̼������e��ֵ��
��� �⣺��I����N������Ϊ��$\frac{8}{3}$��$\frac{2}{3}$����
��$\frac{\frac{64}{9}}{{a}^{2}}$+$\frac{\frac{4}{9}}{{b}^{2}}$=1����$\frac{64}{{a}^{2}}$+$\frac{4}{{b}^{2}}$=9��
��BF22=b2+c2=a2��
��a2=��2$\sqrt{2}$��2=8����b2=4��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
������F1��-c��0����F2��c��0����
��B��0��b����
��ֱ��BF2��y=-$\frac{b}{c}$x+b��
������Բ����$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ã�$\frac{1}{{a}^{2}}$+$\frac{1}{{c}^{2}}$��x2-$\frac{2}{c}$x=0��
���x=0����x=$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$��
��M��$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$��$\frac{b��{c}^{2}-{a}^{2}��}{{a}^{2}+{c}^{2}}$������M��N����x��Գƣ�
��N��$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$��-$\frac{b��{c}^{2}-{a}^{2}��}{{a}^{2}+{c}^{2}}$����
��${k}_{{F}_{1}N}$=-$\frac{\frac{b��{c}^{2}-{a}^{2}��}{{a}^{2}+{c}^{2}}}{\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}+c}$=$\frac{{a}^{2}b-b{c}^{2}}{3{a}^{2}c+{c}^{3}}$��
��F1N��MB��
��$\frac{{a}^{2}b-b{c}^{2}}{3{a}^{2}c+{c}^{3}}$•��-$\frac{b}{c}$��=-1��
��b2=a2-c2��$\frac{{c}^{2}}{{a}^{2}}$=$\frac{1}{5}$��
��e=$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$��
���� ������Ҫ����Բ���ߵ��ۺ����⣬Ҫ������������Բ���̵����Լ�ֱ�ߴ�ֱ��б��֮��Ĺ�ϵ���������ϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 1��4 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y-3=2��x-2�� | B�� | y+3=2��x-2�� | C�� | y-2=k��x+3�� | D�� | y-2=2��x-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
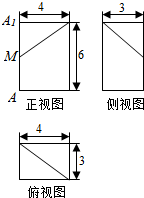 ��ij�����������ͼ��ͼ��ʾ������A1M��AM=7��5����˼������������ڣ�������
��ij�����������ͼ��ͼ��ʾ������A1M��AM=7��5����˼������������ڣ�������| A�� | 55 | B�� | 62 | C�� | 65 | D�� | 72 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com