
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,…,则称
,…,则称![]() 为“绝对差数列”.
为“绝对差数列”.
(1)举出一个前5项不为零的“绝对差数列”(只要求写出前10项);
(2)若“绝对差数列”![]() 中,
中,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,…,分别判断当
,…,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值.
的极限是否存在?如果存在,求出其极限值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: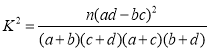
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为实数,
为实数,![]() 为正整数.
为正整数.
(Ⅰ)证明:对任意的实数![]() ,数列
,数列![]() 不是等比数列;
不是等比数列;
(Ⅱ)证明:当![]() 时,数列
时,数列![]() 是等比数列;
是等比数列;
(Ⅲ)设![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在实数
项和,是否存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱![]() 中,AB=1,AC=2,
中,AB=1,AC=2,![]() ,AB⊥AC,
,AB⊥AC,![]() 底面ABC.
底面ABC.
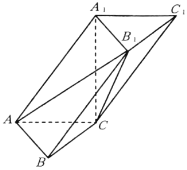
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com