
分析 由三角函数的诱导公式可得f(sinx)=f(cos($\frac{π}{2}$-x))=cosk($\frac{π}{2}$-x),再由两角差的余弦公式,化简整理,即可得到所求k的条件.
解答 解:f(cosx)=coskx(k∈Z),
则f(sinx)=f(cos($\frac{π}{2}$-x))=cosk($\frac{π}{2}$-x)
=cos($\frac{kπ}{2}$-kx)=sinkx,
即有cos$\frac{kπ}{2}$coskx+sin$\frac{kπ}{2}$sinkx=sinkx,
即有sin$\frac{kπ}{2}$=1,cos$\frac{kπ}{2}$=0,
则$\frac{kπ}{2}$=2nπ+$\frac{π}{2}$,n∈Z,
即为k=4n+1,n∈Z.
故答案为:k=4n+1,n∈Z.
点评 本题考查函数的解析式的求法,考查三角函数的诱导公式和两角差的余弦公式的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<λ<1 | B. | λ=0 | C. | λ<0且λ≠-1 | D. | λ≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
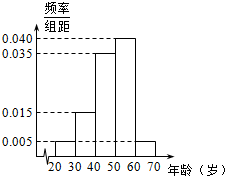 跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.
跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.| 广舞迷 | 非广舞迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com