

(1)当A点在y轴上移动时,求动点M的轨迹C的方程;
(2)已知k∈R,i=(0,1),j=(1,0),经过(-1,0)以ki+j为方向向量的直线l与轨迹C交于E、F两点,又点D(1,0),若∠EDF为钝角时,求k的取值范围.
解:(1)设A(0,y0)、Q(x0,0)、M(x,y),

则![]() =(-3,-y0),
=(-3,-y0),![]() =(x0,-y0).
=(x0,-y0).
又![]() ·
·![]() =0,∴-3x0+(-y0)(-y0)=0.
=0,∴-3x0+(-y0)(-y0)=0.
∴y02=3x0. ①
又|![]() |=2|
|=2|![]() |,
|,
∴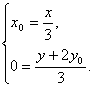 ∴
∴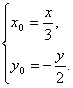 ②
②
将②代入①,有y2=4x(x≠0).
(2)ki+j=k(0,1)+(1,0)=(1,k),
则l:y=k(x+1),与y2=4x联立,
得k2x2+(2k2-4)x+k2=0,
x1+x2=![]() ,x1x2=1.
,x1x2=1.
当Δ>0时,k∈(-1,0)∪(0,1), ③
又![]() =(x1-1,y1),
=(x1-1,y1),![]() =(x2-1,y2),
=(x2-1,y2),
若∠EDF为钝角,则![]() ·
·![]() <0.
<0.
而![]() ·
·![]() =(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+k(x1+1)k(x2+1)+1
=(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+k(x1+1)k(x2+1)+1
=(k2+1)x1x2+(k2-1)(x1+x2)+k2+1<0, ④
将③代入④整理有4k2-2<0.
∴![]() <k<
<k<![]() .
.
由题知k≠0,
∴满足题意k∈(![]() ,0)∪(0,
,0)∪(0,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本小题满分14分)如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)当A点在y轴上移动时,求动点M的轨迹C的方程;
(2)已知k∈R,i=(0,1),j=(1,0),经过(-1,0)以ki+j为方向向量的直线l与轨迹C交于E、F两点,又点D(1,0),若∠EDF为钝角时,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com