[题目]已知正四面体的棱长为.为棱的中点.过作其外接球的截面.则截面面积的最小值为．题目和参考答案——青夏教育精英家教网—

【题目】已知正四面体的棱长为，为棱的中点，过作其外接球的截面，则截面面积的最小值为__________．

【答案】

【解析】将四面体放置于正方体中，可得正方体的外接球就是四面体的外接球，∵正四面体的棱长为，∴正方体的棱长为，可得外接球半径满足，解得，为棱的中点，过作其外接球的截面，当截面到球心的距离最大时，截面圆的面积达最小值，此时球心到截面的距离等于正方体棱长的一半，可得截面圆的半径为，得到截面圆的面积最小值为．

点睛:空间几何体与球接、切问题的求解方法

(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．

(2)若球面上四点构成的三条线段两两互相垂直，且，一般把有关元素“补形”成为一个球内接长方体，利用求解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某市每年中考都要举行实验操作考试和体能测试，初三（1）班共有30名学生，如图表格为该班学生的这两项成绩，表中实验操作考试和体能测试都为优秀的学生人数为6人．由于部分数据丢失，只知道从这班30人中随机抽取一个，实验操作成绩合格，且体能测试成绩合格或合格以上的概率是．

		实验操作
		不合格	合格	良好	优秀
体能测试	不合格	0	1	1	1
	合格	0	2	1
	良好	1		2	4
	优秀	1	1	3	6

（Ⅰ）试确定，的值；

（Ⅱ）从30人中任意抽取3人，设实验操作考试和体能测试成绩都是良好或优秀的学生人数为，求随机变量的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数（）．

（Ⅰ）若，求曲线在处的切线方程；

（Ⅱ）若对任意，，恒成立，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义域为R的函数f（x）= 是奇函数，
（1）求实数a的值；
（2）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求实数k的取值范围；
（3）设关于x的方程f（4x﹣b）+f（﹣2x+1）=0有实数根，求实数b的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的离心率为，过的左焦点的直线，直线被圆：截得的弦长为.

（Ⅰ）求椭圆的方程；

（Ⅱ）设的右焦点为，在圆上是否存在点，满足，若存在，指出有几个这样的点（不必求出点的坐标）；若不存在，说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C：，点P，过右焦点F作与y轴不垂直的直线l交椭圆C于A，B两点.

（Ⅰ ）求椭圆C的离心率；

（Ⅱ ）求证：以坐标原点O为圆心与PA相切的圆，必与直线PB相切.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图：在四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=3，PA⊥底面ABCD，E是PC中点，F是AB中点．

（Ⅰ）求证：BE∥平面PDF；

（Ⅱ）求直线PD与平面PFB所成角的正切值；

（Ⅲ）求三棱锥P﹣DEF的体积．

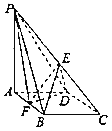
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2﹣4x+a+3，a∈R．
（1）若函数y=f（x）的图象与x轴无交点，求a的取值范围；
（2）若函数y=f（x）在[﹣1，1]上存在零点，求a的取值范围；
（3）设函数g（x）=bx+5﹣2b，b∈R．当a=0时，若对任意的x1∈[1，4]，总存在x2∈[1，4]，使得f（x1）=g（x2），求b的取值范围．