
分析 题意可转化为函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象有且只有一个交点,求导g′(x)=x2-2x=x(x-2),从而确定g(x)的大致形状,从而作函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象,从而结合图象讨论确定交点的个数,从而解得.
解答 解:∵f(x)=13x3-x2+ax-a只有一个零点,
∴函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象有且只有一个交点,
∵g′(x)=x2-2x=x(x-2),
故g(x)在(-∞,0)上是增函数,在(0,2)上是减函数,在(2,+∞)上是增函数,
且g(0)=0,g(2)=83-4=-43;
作函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象如下,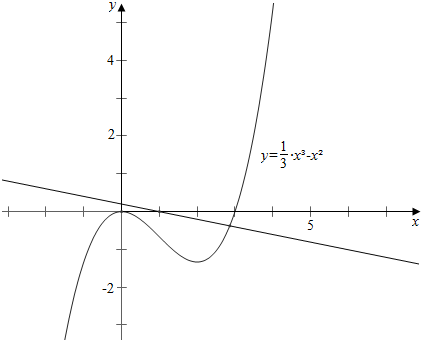 ,
,
结合图象知,当-a<0,即a>0时,
函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象有且只有一个交点,
当-a=0,即a=0时,
函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象有且只有两个交点,
当-a>0,即a<0时,
函数g(x)=13x3-x2与函数h(x)=-a(x-1)的图象有且只有三个交点,
故a的取值范围为(0,+∞).
点评 本题考查了导数的综合应用及数形结合的思想应用,同时考查了函数的零点与函数图象的交点的关系应用.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.
现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com