
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上的一动点,过点
上的一动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)当切线![]() 的长度为
的长度为![]() 时,求线段PM长度.
时,求线段PM长度.
(2)若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 在直线
在直线![]() 上运动时,圆
上运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(3)求线段![]() 长度的最小值.
长度的最小值.

 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第![]() 天的销售价格(单位:元/件)为
天的销售价格(单位:元/件)为![]() ,第
,第![]() 天的销售量(单位:件)为
天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为1200元(
为常数),且在第20天该商品的销售收入为1200元(![]() ).
).
(Ⅰ)求![]() 的值,并求第15天该商品的销售收入;
的值,并求第15天该商品的销售收入;
(Ⅱ)求在这30天中,该商品日销售收入![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
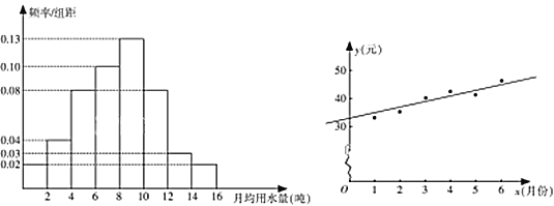
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆M过点P(10,4),且与直线4x+3y-20=0相切于点A(2,4)
(1)求圆M的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且![]() ,求直线l的方程;
,求直线l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不相等的实根;
命题q:函数f(x)=lg[x2﹣2(m+1)x+m(m+1)]的定义域为R,
若“p∨q”为真,“p∧q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com