
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(I)求证:![]() 是等比数列;
是等比数列;
(II)求证:![]() 不是等比数列.
不是等比数列.
【答案】(1) 证明见解析.
(2)证明见解析.
【解析】分析:(I)由![]() ,则
,则![]() 时,
时,![]() ,两式相减,化简得到
,两式相减,化简得到
![]() ,即可得到数理
,即可得到数理![]() 是公比为
是公比为![]() 的等比数列;
的等比数列;
(II)(方法一)由(I)知![]() 是等比数列,所以
是等比数列,所以![]() ,于是
,于是![]() ,解得
,解得![]() ,即可得到数列
,即可得到数列![]() 不是等比数列.
不是等比数列.
(方法二) 由(I)得![]() ,因此
,因此![]() ,求得于是
,求得于是![]() 假设
假设![]() 是等比数列,则有
是等比数列,则有![]() ,解得
,解得![]() ,即可得
,即可得![]() 不是等比数列.
不是等比数列.
详解:(I)因为![]() ,所以当
,所以当![]() 时
时![]() ,
,
两式相减得![]() ,
,
即![]() ,
,
因此![]() ,
,
故![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(II)(方法一)假设![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() .
.
由(I)知![]() 是等比数列,所以
是等比数列,所以![]() ,
,
于是![]() ,即
,即![]() ,解得
,解得![]() ,
,
这与![]() 是等比数列相矛盾,
是等比数列相矛盾,
故假设错误,即![]() 不是等比数列.
不是等比数列.
(方法二) 由(I)知![]() ,所以
,所以![]() ,因此
,因此![]() .
.
于是![]() ,
,
假设![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() ,解得
,解得![]() ,
,
这与![]() 相矛盾,
相矛盾,
故假设错误,即![]() 不是等比数列.
不是等比数列.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:
【题目】若存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),an+1= , 关于下列命题:
, 关于下列命题:
①当m=![]() 时,a5=2
时,a5=2
②若m=![]() , 则数列{an}是周期为3的数列;
, 则数列{an}是周期为3的数列;
③对若a2=4,则m可以取3个不同的值;
④m∈Q且m∈[4,5],使得数列{an}是周期为6.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某渔船在渔港O的南偏东60°方向,距离渔港约160海里的B处出现险情,此时在渔港的正上方恰好有一架海事巡逻飞机A接到渔船的求救信号,海事巡逻飞机迅速将情况通知了在C处的渔政船并要求其迅速赶往出事地点施救.若海事巡逻飞机测得渔船B的俯角为68.20°,测得渔政船C的俯角为63.43°,且渔政船位于渔船的北偏东60°方向上.
(Ⅰ)计算渔政船C与渔港O的距离;
(Ⅱ)若渔政船以每小时25海里的速度直线行驶,能否在3小时内赶到出事地点?
(参考数据:sin68.20°≈0.93,tan68.20°≈2.50,shin63.43°≈0.90,tan63.43°≈2.00, ![]() ≈3.62,
≈3.62, ![]() ≈3.61)
≈3.61)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学教职工春季竞走比赛在校田径场隆重举行,为了解高三年级男、女两组教师的比赛用时情况,体育组教师从两组教师的比赛成绩中,分别各抽取9名教师的成绩(单位:分钟),制作成下面的茎叶图,但是女子组的数据中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示,规定:比赛用时不超过19分钟时,成绩为优秀.
(1)若男、女两组比赛用时的平均值相同,求a的值;
(2)求女子组的平均用时高于男子组平均用时的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
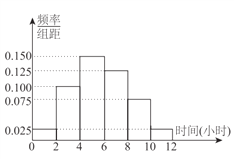
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() x3+sinx+2x的定义域为R,数列{an}是公差为d的等差数列,且a1+a2+a3+a4+…a2015<0,记m=f(a1)+f(a2)+f(a3)+…f(a2015),关于实数m,下列说法正确的是( )
x3+sinx+2x的定义域为R,数列{an}是公差为d的等差数列,且a1+a2+a3+a4+…a2015<0,记m=f(a1)+f(a2)+f(a3)+…f(a2015),关于实数m,下列说法正确的是( )
A.m恒为负数
B.m恒为正数
C.当d>0时,m恒为正数;当d<0时,m恒为负数
D.当d>0时,m恒为负数;当d<0时,m恒为正数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量![]() (单位:千克)与施用肥料
(单位:千克)与施用肥料![]() (单位:千克)满足如下关系:
(单位:千克)满足如下关系: ,肥料成本投入为
,肥料成本投入为![]() 元,其它成本投入(如培育管理、施肥等人工费)
元,其它成本投入(如培育管理、施肥等人工费)![]() 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为
元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为![]() (单位:元).
(单位:元).
(Ⅰ)求![]() 的函数关系式;
的函数关系式;
(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com