本小题共13分)
对数列

,规定
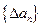
为数列

的一阶差分数列,其中
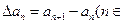
N
*).对正整数
k,规定
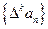
为

的
k阶差分数列,其中
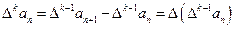
.
(Ⅰ)若数列

的首项
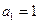
,且满足

,求数列

的通项公式;
(Ⅱ)对(Ⅰ)中的数列

,若数列
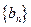
是等差数列,使得
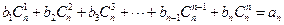
对一切正整数
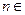
N
*都成立,求
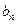
;
(Ⅲ)在(Ⅱ)的条件下,令
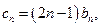
设

若
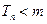
成立,求最小正整数
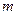
的值.
解:(Ⅰ)由

及
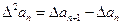
,
得
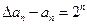
,
∴
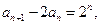
∴
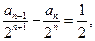
———————————————2分
∴数列
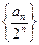
是首项为
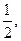
公差为
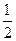
的等差数列,
∴
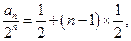
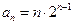
.————————4分
(Ⅱ)∵
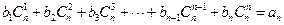
,
∴
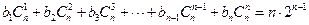
.
∵
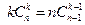
,
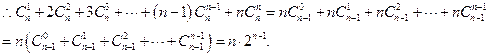
∴

.————————————9分
(Ⅲ)由(Ⅱ)得
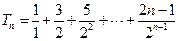
, ①
有
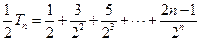
, ②
①-② 得
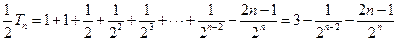
,
∴
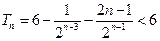
, ——————————10分
又
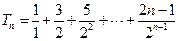
,
∴
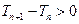
,
∴
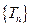
是递增数列,且
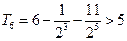
,
∴ 满足条件的最小正整数
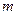
的值为6.————————13分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知数列
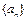
的首项
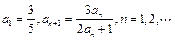
.
(Ⅰ)求
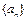
的通项公式;
(Ⅱ)证明:对任意的
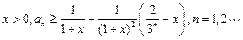
;
(Ⅲ)证明:
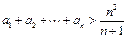
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题14分)
(I)已知数列
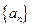
满足
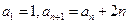
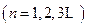
,
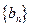
满足
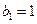
,

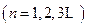
,求证:
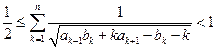
。.
(II) 已知数列
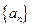
满足:a
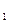
=1且
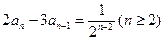
。设m
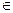
N

,m
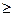
n
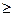
2,证明(a
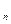
+
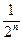
)
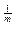
(m-n+1)
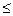
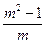

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知数列
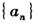
的前n项和
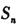
满足
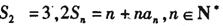
.
(2) 求
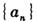
的通项公式,并求数列
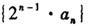
的前n项和
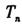
;
(3) 设
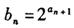
,证明:
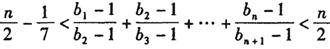
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列
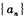
中,
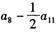
=6,则数列的前9项之和等于( )
| A.24 | B.48  | C.72 | D. 108 108 |
查看答案和解析>>

 ,规定
,规定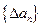 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中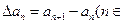 N*).对正整数k,规定
N*).对正整数k,规定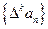 为
为 的k阶差分数列,其中
的k阶差分数列,其中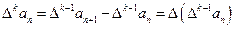 .
. 的首项
的首项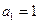 ,且满足
,且满足 ,求数列
,求数列 的通项公式;
的通项公式; ,若数列
,若数列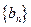 是等差数列,使得
是等差数列,使得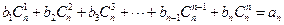 对一切正整数
对一切正整数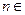 N*都成立,求
N*都成立,求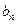 ;
;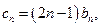 设
设 若
若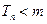 成立,求最小正整数
成立,求最小正整数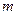 的值.
的值. 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案