Question

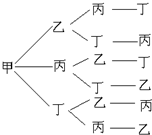
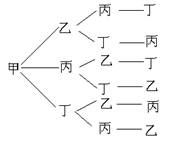
为加强中学生实践、创新能力和团队精神的培养，促进教育教学改革，教育部门主办了全国中学生航模竞赛．该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序．通过预赛，选拔出甲、乙、丙和丁四支队伍参加决赛．
（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；
（ II）求决赛中甲、乙两支队伍出场顺序相邻的概率．

Answer 1

分析：列举总的基本事件数，设“甲、乙两支队伍恰好排在前两位”为事件A，“甲、乙两支队伍出场顺序相邻”为事件B，分析可得A、B包含的基本事件数目，由等可能事件的概率公式，计算可得答案．

解答：解：利用树状图列举如右图，这是以甲开头的，
还有分别以乙、丙、丁开头的也都有6种情况．
故总共有24个基本事件，
符合（Ⅰ）要求的有4个基本事件，符合（ II）要求的有12个基本事件，
所以所求的概率分别为

1

6

，

1

2

．
另解：（Ⅰ）由排列组合的公式可得“甲、乙两支队伍恰好排在前两位”的概率P=

A 2 2 A 2 2

A 4 4

=

1

6

（ II）同理可得，“甲、乙两支队伍出场顺序相邻”的概率为

A 3 3 A 2 2

A 4 4

=

1

2

点评：本题考查等可能事件概率的计算，关键是根据题意，正确列举基本事件空间，得到其包含基本事件的数目．