练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    定义max{a，b}=
    a，a≥b
    b，a＜b
    ，设实数x，y满足约束条件
    |x|≤2
    |y|≤2
    ，z=max{2x-y，3x+y}    ，则z的取值范围是（　　）
    分析：由题意可得约束条件所满足的可行域如图所示的正方形ABCD，由Z=
    2x-y，x+2y≤0
    3x+y，x+2y＞0

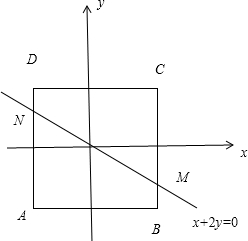
    当x+2y＜0时的可行域即为图中的四边形ABMN，Z=2x-y在N（-2，1）处取得最小值-5，在B（2，-2）处取得最大值6；当x+2y≥0时的可行域为图中的四边形MCDN，Z=3x+y在C（2，2）处取得最小值8，从而可求Z的取值范围
    解答：解：由题意可得约束条件所满足的可行域如图所示的正方形ABCD
    由Z=
    2x-y，x+2y≤0
    3x+y，x+2y＞0

    当x+2y＜0时的可行域即为图中的四边形ABMN，Z=2x-y在N（-2，1）处取得最小值-5，在B（2，-2）处取得最大值6
    当x+2y≥0时的可行域为图中的四边形MCDN，Z=3x+y在C（2，2）处取得最小值8
    ∴-5≤Z≤8
    故选：C
    点评：本题主要考查了简单的线性规划，解题的关键是要根据题目中的定义确定目标函数及可行域的条件以及，属于知识的综合应用题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    定义max{a，b}=
    a(a≥b)
    b(a＜b)
    ，已知实数x，y满足|x|≤1，|y|≤1，设z=max{x+y，2x-y}，则z的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的是
    ②③⑤
    ②③⑤
    ．（只填正确说法序号）
    ①若集合A={y|y=x-1}，B={y|y=x2-1}，则A∩B={（0，-1），（1，0）}；
    ②函数y=f（x）的图象与x=a（a∈R）的交点个数只能为0或1；
    ③f(x)=lg(x+
    		x2+1
    )    是定义在R上的奇函数；
    ④若函数f（x）在（-∞，0]，（0，+∞）都是单调增函数，则f（x）在（-∞，+∞）上也是增函数；
    ⑤定义max(a，b)=
    a，(a≥b)
    b，(a＜b)
    ，则f（x）=max（x+1，4-2x）的最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义max(a，b)=
    aa≥b
    ba＜b
    ，已知x、y满足条件
    x+2≥0
    y≥0
    x+y≤2
    ，若z=max（3x-y，4x-2y），则z的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义max{a，b，c}为a、b、c中的最大者，令M=max{|1+a+2b|，|1+a-2b|，|2+b|}，则对任意实数a，b，M的最小值是（　　）

    查看答案和解析>>

    同步练习册答案