
【题目】若函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),其坐标满足条件:|x1x2+y1y2|﹣ ![]() 的最大值为0,则称f(x)为“柯西函数”, 则下列函数:
的最大值为0,则称f(x)为“柯西函数”, 则下列函数:
①f(x)=x+ ![]() (x>0);
(x>0);
②f(x)=lnx(0<x<3);
③f(x)=2sinx;
④f(x)= ![]() .
.
其中为“柯西函数”的个数为( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:由柯西不等式得:对任意实数x1 , y1 , x2 , y2 , |x1x2+y1y2|﹣ ![]() ≤0恒成立(当且仅当存在实数k,使得x1=kx2 , y1=ky2取等号),若函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),其坐标满足条件:|x1x2+y1y2|﹣
≤0恒成立(当且仅当存在实数k,使得x1=kx2 , y1=ky2取等号),若函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),其坐标满足条件:|x1x2+y1y2|﹣ ![]() 的最大值为0,则函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),使得
的最大值为0,则函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),使得 ![]() 共线,即存在点A、B与点O共线; 对于①,f(x)=x+
共线,即存在点A、B与点O共线; 对于①,f(x)=x+ ![]() (x>0)存在;
(x>0)存在;
对于②,f(x)=lnx ![]() (0<x<3)不存在;
(0<x<3)不存在;
对于③,f(x)=2sinx存在;
对于④,f(x)= ![]() 存在.
存在.
故选:C.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖,求下列问题:(1)求顾客抽奖1次能获奖的概率(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为 X ,求 X 的分布列和数学期望.
(1)(1)求顾客抽奖1次能获奖的概率
(2)(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() , 求
, 求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为4,最小值为1.
上的最大值为4,最小值为1.
(1)求实数![]() 、
、![]() 的值;
的值;
(2)记![]() ,若
,若![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)对于函数![]() ,用
,用![]() ,1,2,
,1,2,![]() ,
,![]() ,
,![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,若存在常数
个小区间,若存在常数![]() ,使得和式
,使得和式![]() 对任意的划分恒成立,则称函数
对任意的划分恒成立,则称函数![]() 为
为![]() 上的有界变差函数.记
上的有界变差函数.记![]() ,试判断函数
,试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
(参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中 ![]() 中,已知曲线
中,已知曲线 ![]() 经过点
经过点 ![]() ,其参数方程为
,其参数方程为 ![]() (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)若直线 ![]() 交
交 ![]() 于点
于点 ![]() ,且
,且 ![]() ,求证:
,求证: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正三棱柱ABC﹣A1B1C1底边长为2,E,F分别为BB1 , AB的中点. (I)已知M为线段B1A1上的点,且B1A1=4B1M,求证:EM∥面A1FC;
(II)若二面角E﹣A1C﹣F所成角的余弦值为 ![]() ,求AA1的值.
,求AA1的值.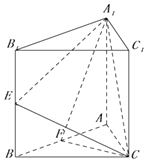
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对于定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”.下列结论中正确的个数为( )
特征函数”.下列结论中正确的个数为( )
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”.
特征函数”.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点. 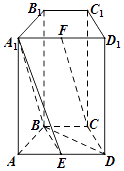
(Ⅰ)求证:DD1⊥平面ABCD;
(Ⅱ)求证:平面A1BE⊥平面ADD1A1;
(Ⅲ)若CF∥平面A1BE,求棱BC的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2. 
(Ⅰ)求证:平面EBD⊥平面BCF;
(Ⅱ)求点B到平面ECD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com