
【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:
资源\消耗量\产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤(t) | 9 | 4 | 360 |
电力(kwh) | 4 | 5 | 200 |
劳动力(个) | 3 | 10 | 300 |
利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=|x|,g(x)= ![]()
B.f(x)=lg x2 , g(x)=2lg x
C.f(x)= ![]() ,g(x)=x+1
,g(x)=x+1
D.f(x)= ![]() ?
? ![]() ,g(x)=
,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC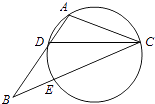
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
(1)命题![]() ,使得
,使得![]() ,则
,则![]() ,都有
,都有![]() ;
;
(2)已知函数f(x)=|log2x|,若a≠b,且f(a)=f(b),则ab=1;
(3)若平面α内存在不共线的三点到平面β的距离相等,则平面α平行于平面β;
(4)已知定义在![]() 上的函数
上的函数![]() 满足条件
满足条件![]() ,且函数
,且函数![]() 为奇函数,则函数
为奇函数,则函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
其中真命题的序号为______________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com