
【题目】设函数![]() .
.
(1)证明:![]() ,
,![]() ;
;
(2)令![]()
①求![]() 的最大值;
的最大值;
②如果![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)证明见解析;(2)①![]() 的最大值为
的最大值为![]() ;②证明见解析
;②证明见解析![]() .
.
【解析】
(1)令![]() ,则
,则![]() ,利用导数求出函数
,利用导数求出函数![]() 的单调性与最值,由此可证明结论;
的单调性与最值,由此可证明结论;
(2)由题意得![]() ,
,![]() ,
,
①利用导数求出函数的单调性,从而得到函数的极值与最值;
②由题意不妨设![]() ,又
,又![]() ,可得
,可得![]() ,令
,令![]() ,
,![]() ,利用导数可得函数
,利用导数可得函数![]() 在
在![]() 上单调递增,从而可推出
上单调递增,从而可推出![]() ,结合条件可得
,结合条件可得![]() ,易得
,易得![]() ,从而借助函数
,从而借助函数![]() 在
在![]() 上单调递增即可证明.
上单调递增即可证明.
(1)证明:令![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 处取得极大值,也是最大值,
处取得极大值,也是最大值,
∴![]() ,
,
即![]() ,
,![]() ;
;
(2)解:![]()
![]() ,
,![]() ,
,
①由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 处取得极大值,也是最大值,
处取得极大值,也是最大值,
∴![]() 的最大值
的最大值![]() ;
;
②由![]() ,不妨设
,不妨设![]() ,又
,又![]() ,
,
∵当![]() 时,
时,![]() ,且
,且![]() ,
,
∴![]() ,
,
令![]()
![]() ,
,![]() ,
,
则![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
∴当![]() 时,
时,![]() ,
,
即![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
而函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=![]() ,BC=CD=BD=2
,BC=CD=BD=2![]() ,则球O的表面积为( )
,则球O的表面积为( )
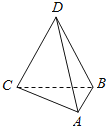
A.4π B.12π C.16π D.36π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).

|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧开一壶水时间
哪一个更适宜作烧开一壶水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立关于
![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时烧开一壶水最省煤气?
为多少时烧开一壶水最省煤气?
附:对于一组数据![]()
![]()
![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为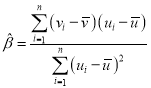 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,则在圆
,则在圆![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,使得
,使得![]() ,
,![]() ?若存在,请求出
?若存在,请求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内与两定点![]() ,
,![]() 连线的斜率之积等于
连线的斜率之积等于![]() 的点的轨迹,加上
的点的轨迹,加上![]() 、
、![]() 两点所成的曲线为
两点所成的曲线为![]() .若曲线
.若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 、
、![]() 满足
满足![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).该小组在操场上选定A点,此时测量视线和铅锤线之间的夹角在量角器上度数为37°;推动自行车直线后退,轮子滚动了10卷达到B点,此时测量视线和铅锤线之间的夹角在量角器上度数为53°.测量者站立时的“眼高”为1.55m,根据以上数据可计算得该建筑物的高度约为___________米.(精确到0.1)
参考数据:![]() ,
,![]()
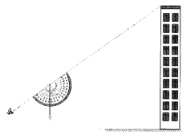
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() (
(![]() 为自然对数的底数)处的切线方程;
为自然对数的底数)处的切线方程;
(2)若对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 为
为![]() 在区间
在区间![]() 上的下界函数,
上的下界函数,![]() 为
为![]() 在区间
在区间![]() 上的上界函数.
上的上界函数.
①若![]() ,求证:
,求证:![]() 为
为![]() 在
在![]() 上的上界函数;
上的上界函数;
②若![]() ,
,![]() 为
为![]() 在
在![]() 上的下界函数,求实数
上的下界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对
的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对![]() ,再统计两数能与1构成钝角三角形三边的数对
,再统计两数能与1构成钝角三角形三边的数对![]() 的个数m;最后再根据计数m来估计π的值.假设统计结果是
的个数m;最后再根据计数m来估计π的值.假设统计结果是![]() ,那么可以估计
,那么可以估计![]() 的近似值为____________.(用分数表示)
的近似值为____________.(用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com