
【题目】定义“正对数”:ln+x= ![]() ,现有四个命题:
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则 ![]() ;
;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2.
其中的真命题有(写出所有真命题的序号)
【答案】①③④
【解析】解:(1)对于①,由定义,当a≥1时,ab≥1,故ln+(ab)=ln(ab)=blna,又bln+a=blna,故有ln+(ab)=bln+a;当a<1时,ab<1,故ln+(ab)=0,又a<1时bln+a=0,所以此时亦有ln+(ab)=bln+a,故①正确;
(2)对于②,此命题不成立,可令a=2,b= ![]() ,则ab=
,则ab= ![]() ,由定义ln+(ab)=0,ln+a+ln+b=ln2,所以ln+(ab)≠ln+a+ln+b,故②错误;
,由定义ln+(ab)=0,ln+a+ln+b=ln2,所以ln+(ab)≠ln+a+ln+b,故②错误;
(3)对于③,
i. ![]() ≥1时,此时
≥1时,此时 ![]() ≥0,
≥0,
当a≥b≥1时,ln+a﹣ln+b=lna﹣lnb= ![]() ,此时则
,此时则 ![]() ,命题成立;
,命题成立;
当a>1>b>0时,ln+a﹣ln+b=lna,此时 ![]() ,
, ![]() >lna,则
>lna,则 ![]() ,命题成立;
,命题成立;
当1>a≥b>0时,ln+a﹣ln+b=0, ![]() 成立;
成立;
ii. ![]() <1时,同理可验证是正确的,故③正确;
<1时,同理可验证是正确的,故③正确;
(4)对于④,
当a≥1,b≥1时,ln+(a+b)=ln(a+b),ln+a+ln+b+ln2=lna+lnb+ln2=ln(2ab),
∵a+b﹣2ab=a﹣ab+b﹣ab=a(1﹣b)+b(1﹣a)≤0,
∴a+b≤2ab,
∴ln(a+b)<ln(2ab),
∴ln+(a+b)≤ln+a+ln+b+ln2.
当a>1,0<b<1时,ln+(a+b)=ln(a+b),ln+a+ln+b+ln2=lna+ln2=ln(2a),
∵a+b﹣2a=b﹣a≤0,
∴a+b≤2a,
∴ln(a+b)<ln(2a),
∴ln+(a+b)≤ln+a+ln+b+ln2.
当b>1,0<a<1时,同理可证ln+(a+b)≤ln+a+ln+b+ln2.
当0<a<1,0<b<1时,可分a+b≥1和a+b<1两种情况,均有ln+(a+b)≤ln+a+ln+b+ln2.
故④正确.
所以答案是①③④.
【考点精析】关于本题考查的命题的真假判断与应用,需要了解两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能得出正确答案.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某公路AB一侧有一块空地△OAB,其中OA=3km,OB=3![]() km,∠AOB=90°.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
km,∠AOB=90°.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.

(1)若M在距离A点2km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH. 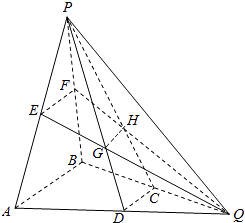
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧 ![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com