
【题目】连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2 ![]() 和4
和4 ![]() ,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为 .
【答案】①③④
【解析】解:②错误.易求得M、N到球心O的距离分别为3、2,
若两弦交于N,则OM⊥MN,Rt△OMN中,有OM<ON,矛盾.
分别取球O的两条弦AB、CD的中点E、F,则OE= ![]() ,OF=
,OF= ![]() ,
,
即可以看做弦AB、CD分别是球半径为3和2的球的切线,且弦AB在半径为2的球的外部,
弦AB与CD只可能相交与M点,且MN的最大距离为2+3=5,最小距离为3﹣2=1,当M、O、N共线时分别取最大值5最小值1.
综上可得正确的命题的序号为①③④.
所以答案是:①③④.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
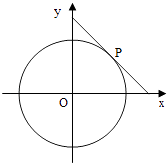
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() ﹣
﹣ ![]() =1过点P且离心率为
=1过点P且离心率为 ![]() .
. 
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,有几个正确( )
①ED⊥平面ACD ②CD⊥平面BED ③BD⊥平面ACD ④AD⊥平面BED.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角为60°;
其中正确结论是(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm的内接圆柱. 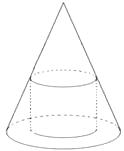
(1)试用x表示圆柱的侧面积;
(2)当x为何值时,圆柱的侧面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
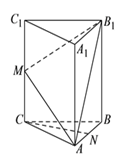
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长
的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com