
已知直线的倾斜角的取值范围,利用正切函数的性质,讨论直线斜率及其绝对值的变化情况:
(1)0°<α<90°
(2)90°<α<180°
解:(1)作出y=tanα在(0°,90°)区间内的函数图象;
由图象观察可知: 当α∈(0°,90°),y=tanα>0,并且随着α的增大,y不断增大,|y|也不断增大。 所以,当α∈(0°,90°)时,随着倾斜角α的不断增大,直线斜率不断增大,直线斜率的绝对值也不断增大。 (2)作出y=tanα在(90°,180°)区间内的函数图象,
由图象观察可知: 当α∈(90°,180°),y=tanα<0,并且随着α的增大,y=tanα不断增大,|y|不断减小。 所以当α∈(90°,180°)时,随着倾斜角α的不断增大,直线的斜率不断增大,但直线斜率的绝对值不断减小。 |


科目:高中数学 来源: 题型:
| 3 |
| π |
| 3 |
| 3π |
| 4 |
| π |
| 3 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)0°<α<90°
(2)90°<α<180°
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省台州市高二(下)期末数学试卷(文科)(解析版) 题型:解答题
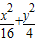 =1的左、右顶点分别为A、B,曲线E是以椭圆中心为顶点,B为焦点的抛物线.
=1的左、右顶点分别为A、B,曲线E是以椭圆中心为顶点,B为焦点的抛物线.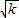 (x-2)与曲线E交于不同的两点M、N,当
(x-2)与曲线E交于不同的两点M、N,当 •
• ≥68时,求直线l的倾斜角θ的取值范围.
≥68时,求直线l的倾斜角θ的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com