
【题目】已知函数y=f(x)是R上的偶函数,当x1 , x2∈(0,+∞)时,都有(x1﹣x2)[f(x1)﹣f(x2)]<0.设 ![]() ,则( )
,则( )
A.f(a)>f(b)>f(c)
B.f(b)>f(a)>f(c)
C.f(c)>f(a)>f(b)
D.f(c)>f(b)>f(a)
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC, AB⊥BC, BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE, AC, DE,得到如图所示的空间几何体.
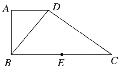
(1)求证:AB⊥平面ADC;
(2)若AD=1,AB=![]() ,求点B到平面ADE的距离.
,求点B到平面ADE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
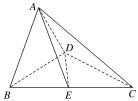
【题目】已知四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 
(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空中有一气球,在它的正西方A点测得它的仰角为45°,同时在它南偏东60°的B点,测得它的仰角为30°,已知A、B两点间的距离为107米,这两个观测点均离地1米,则测量时气球离地的距离是_____米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M( ![]() ,0),N(2,0),曲线C上的任意一点P满足:
,0),N(2,0),曲线C上的任意一点P满足: ![]()
![]() =
= ![]() |
| ![]() |.
|.
(Ⅰ)求曲线C的方程;
(Ⅱ)设曲线C与x轴的交点分别为A、B,过N的任意直线(直线与x轴不重合)与曲线C交于R、Q两点,直线AR与BQ交于点S.问:点S是否在同一直线上?若是,请求出这条直线的方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(I)根据已知数据,把表格数据填写完整;
(II)利用(1)完成的表格数据回答下列问题:
(ⅰ)能否在犯错误的概率不超过0.001的前提下认为性别与支持申办足球世界杯有关;
(ⅱ)已知在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取3人,求至多有1位老师的概率。
附:![]() ,其中
,其中![]()
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P(1,
=1(a>b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P(1, ![]() )在椭圆上,连接PF1交y轴于点Q,点Q满足
)在椭圆上,连接PF1交y轴于点Q,点Q满足 ![]() =
= ![]() .直线l不过原点O且不平行于坐标轴,l与椭圆C有两个交点A,B. (Ⅰ)求椭圆C的标准方程;
.直线l不过原点O且不平行于坐标轴,l与椭圆C有两个交点A,B. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点M( ![]() ,0),若直线l过椭圆C的右焦点F2 , 证明:
,0),若直线l过椭圆C的右焦点F2 , 证明: ![]()
![]() 为定值;
为定值;
(Ⅲ)若直线l过点(0,2),设N为椭圆C上一点,且满足 ![]() +
+ ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足 ![]() ,
, ![]() ,其中n∈N+ . (I)求证:数列{bn}是等差数列,并求出数列{an}的通项公式;
,其中n∈N+ . (I)求证:数列{bn}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,求数列{cncn+2}的前n项和为Tn .
,求数列{cncn+2}的前n项和为Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com