设一元二次方程x2+Bx+C=0,若B、C是一枚骰子先后掷两次出现的点数,求方程有实根的概率.
【答案】
分析:根据B、C是一枚骰子先后掷两次出现的点数,可得(B,C)一共有36种情况.分B=2、3、4、5、6五种情况分别求得C的值,可得满足条件的(B,C)一共有19种情况,
从而求得方程有实数根的概率.
解答:解:∵B、C是一枚骰子先后掷两次出现的点数,∴一共有36种情况.
又由方程有实数解,可得B
2-4C≥0,显然B≠1.
当B=2时,C=1; 共有1种情况.
当B=3时,C=1,2; 共有2种情况.
当B=4时,C=1,2,3,4; 共有4种情况.
当B=5时,C=1,2,3,4,5,6; 共有6种情况.
当B=6时,C=1,2,3,4,5,6; 共有6种情况.
故方程有实数根共有19种情况,
∴方程有实数根的概率是
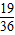
.
点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,体现了分类讨论的数学思想,属于中档题.

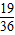 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案