
 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.分析 (1)由直棱柱可得BB1⊥平面ABC,得出BB1⊥AE,由等边三角形性质可得AE⊥BC,故而AE⊥平面BCC1B1,于是平面AEF⊥平面B1BCC1;
(2)由(1)的证明同理可得CD⊥平面ABB1A1,故而CD⊥A1D,∴A1D=CD,利用勾股定理求出AA1从而得出棱锥的高CF,代入棱锥的体积公式计算即可.
解答  解:(1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,所以AE⊥BB1.
解:(1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,所以AE⊥BB1.
又E是正三角形ABC的边BC的中点,所以AE⊥BC.又BC∩BB1=B,
所以AE⊥平面B1BCC1,而AE?平面AEF,
所以平面AEF⊥平面B1BCC1.…(4分)
(2)解:因为△ABC是正三角形,所以CD⊥AB.
又三棱柱ABC-A1B1C1是直三棱柱,所以CD⊥AA1.
所以CD⊥平面A1ABB1,所以CD⊥A1D.
由题可知,∠CA1D=30°,所以A1D=$\sqrt{3}$CD=$\frac{3}{2}$AB=6.
在Rt△AA1D中,AA1=$\sqrt{{A}_{1}{D}^{2}-A{D}^{2}}=\sqrt{36-4}=4\sqrt{2}$,所以FC=$\frac{1}{2}$AA1=2$\sqrt{2}$.
故三棱锥F-AEC的体积V1=$\frac{1}{3}×2\sqrt{3}×2\sqrt{2}=\frac{4\sqrt{6}}{3}$ …(8分)
设A1C∩AF=G,AE∩CD=O,
过G作GH⊥AC于H,连接OG.
∵△A1GA∽△CGF,∴$\frac{CG}{{A}_{1}G}=\frac{CF}{{A}_{1}A}=\frac{1}{2}$
∴$GH=\frac{1}{3}A{A}_{1}=\frac{4\sqrt{2}}{3}$.…(9分)
∴$OD=\frac{1}{2}OC$
∴${{S}_{△}}_{AOC}=\frac{1}{3}{S}_{△ABC}=\frac{4\sqrt{3}}{3}$.…(10分)
三棱锥F-AEC与三棱锥A1-ACD的公共部分为三棱锥G-AOC,…(11分)
V2=$\frac{1}{3}×\frac{4\sqrt{2}}{3}×\frac{4\sqrt{3}}{3}=\frac{16\sqrt{6}}{27}$,
V1-V2=$\frac{4\sqrt{6}}{3}-\frac{16\sqrt{6}}{27}=\frac{20\sqrt{6}}{27}$.…(12分)
点评 本题考查了正三棱柱的结构特征,面面垂直的判定,棱锥的体积计算,属于中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
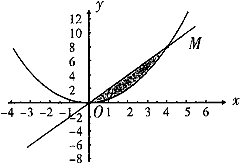 设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )
设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )| A. | 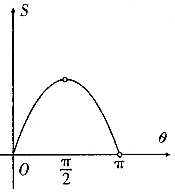 | B. | 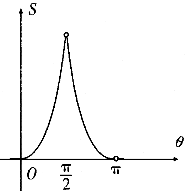 | ||
| C. | 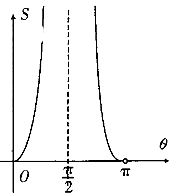 | D. | 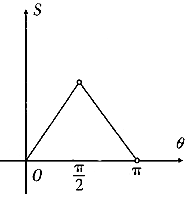 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com