[题目]已知椭圆: . 左右焦点分别为F1 . F2 . 过F1的直线l交椭圆于A.B两点.若|BF2|+|AF2|的最大值为5.则b的值是题目和参考答案——青夏教育精英家教网—

【题目】已知椭圆：，左右焦点分别为F1 ， F2 ，过F1的直线l交椭圆于A，B两点，若|BF2|+|AF2|的最大值为5，则b的值是

【答案】
【解析】解：由0＜b＜2可知，焦点在x轴上，
∵过F1的直线l交椭圆于A，B两点，∴|BF2|+|AF2|+|BF1|+|AF1|=2a+2a=4a=8
∴|BF2|+|AF2|=8﹣|AB|．
当AB垂直x轴时|AB|最小，|BF2|+|AF2|值最大，
此时|AB|=b2 ， ∴5=8﹣b2 ，
解得b= ．
故答案为．
由题意可知椭圆是焦点在x轴上的椭圆，利用椭圆定义得到|BF2|+|AF2|=8﹣|AB|，再由过椭圆焦点的弦中通径的长最短，可知当AB垂直于x轴时|AB|最小，把|AB|的最小值b2代入|BF2|+|AF2|=8﹣|AB|，由|BF2|+|AF2|的最大值等于5列式求b的值．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ln（x+ ），
（1）判断并证明函数y=f（x）的奇偶性；
（2）判断并证明函数y=f（x）在R上的单调性；
（3）当x∈[1，2]时，不等式f（a4x）+f（2x+1）＞0恒成立，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在[50，60）的学生人数为6．
（Ⅰ）求直方图中x的值；
（Ⅱ）试估计所抽取的数学成绩的平均数；
（Ⅲ）试根据样本估计“该校高一学生期末数学考试成绩≥70”的概率．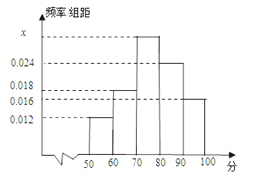

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】非空集合G关于运算⊕满足：
（1）对任意a，b∈G，都有a+b∈G；
（2）存在e∈G使得对于一切a∈G都有a⊕e=e⊕a=a，
则称G是关于运算⊕的融洽集，
现有下列集合与运算：
①G是非负整数集，⊕：实数的加法；
②G是偶数集，⊕：实数的乘法；
③G是所有二次三项式构成的集合，⊕：多项式的乘法；
④G={x|x=a+b ，a，b∈Q}，⊕：实数的乘法；
其中属于融洽集的是（请填写编号）