
【题目】如图,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F为椭圆C的右焦点.A(-a,0),|AF|=3.
,F为椭圆C的右焦点.A(-a,0),|AF|=3.

(I)求椭圆C的方程;
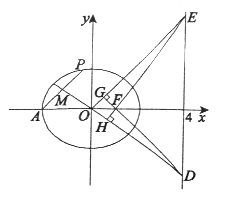
(II)设O为原点,P为椭圆上一点,AP的中点为M.直线OM与直线x=4交于点D,过O且平行于AP的直线与直线x=4交于点E.求证:∠ODF=∠OEF.
【答案】.(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(1)根据椭圆的离心率为![]() ,
, ![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆C的方程;(2)设直线
,即可得椭圆C的方程;(2)设直线![]() 的方程为:
的方程为: ![]() ,将其代入椭圆方程,整理得
,将其代入椭圆方程,整理得![]() ,根据韦达定理可得
,根据韦达定理可得![]() (
(![]() ,
, ![]() ),直线
),直线![]() 的方程是
的方程是![]() ,令
,令![]() ,得
,得![]() ,同理可得
,同理可得![]() ,根据斜率公式可得在
,根据斜率公式可得在![]() 和
和![]() 中,
中, ![]() 和
和![]() 都与
都与![]() 互余,所以
互余,所以![]() .
.
试题解析:(I)设椭圆C的半焦距为c.依题意,得
![]() ,a+c=3. 解得a=2,c=1.
,a+c=3. 解得a=2,c=1.
所以b2=a2-c2=3,所以椭圆C的方程是![]()
(II)由(I)得A(-2,0).设AP的中点M(x0,y0),P(x1,y1).
设直线AP的方程为:y=k(x+2)(k≠0),将其代入椭圆方程,整理得
(4k2+3)x2+16k2x+16k2-12=0,
所以-2+x1=![]() .
.
所以x0=![]() ,y0=k(x0+2)=
,y0=k(x0+2)=![]() ,
,
即M(![]() ,
, ![]() ).
).
所以直线OM的斜率是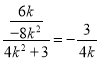 ,
,
所以直线OM的方程是y=-![]() x.令x=4,得D(4,-
x.令x=4,得D(4,-![]() ).
).
直线OE的方程是y=kx.令x=4,得E(4,4k).
由F(1,0),得直线EF的斜率是![]() =
=![]() ,所以EF⊥OM,记垂足为H;
,所以EF⊥OM,记垂足为H;
因为直线DF的斜率是![]() =
=![]() ,所以DF⊥OE,记垂足为G.
,所以DF⊥OE,记垂足为G.
在Rt△EHO和Rt△DGO中,∠ODF和∠OEF都与∠EOD互余,
所以∠ODF=∠OEF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥PDCE的外接球的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
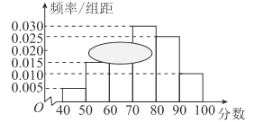
(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都为50%,现采用随机模拟的方法估计该运动员四次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,2,3,4表示命中,5,6,7,8 9表示不命中;再以每四个随机数为一组,代表四次投篮的结果.经随机模拟产生了20组随机数:9075 9660 1918 9257 2716 9325 8121 4589 5690 6832 4315 2573 3937 9279 5563 4882 7358 1135 1587 4989
据此估计,该运动员四次投篮恰有两次命中的概率为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(Ⅰ)求椭圆![]() 的标准方程和长轴长;
的标准方程和长轴长;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 的左焦点,
的左焦点, ![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线交椭圆
的垂线交椭圆![]() 于
于![]() ,记
,记![]() 分别为点
分别为点![]() 和
和![]() 到直线
到直线![]() 的距离,证明
的距离,证明![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com