
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() ,
,![]() ,且
,且![]() ,关于
,关于![]() 的方程
的方程![]() 有唯一实数解,求实数
有唯一实数解,求实数![]() 的值.
的值.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入函数
代入函数![]() 的解析式,求出该函数的定义域与导数,利用导数能求出函数
的解析式,求出该函数的定义域与导数,利用导数能求出函数![]() 的单调增区间与减区间;
的单调增区间与减区间;
(2)由题意知,方程![]() 有唯一实数解,由参变量分离法得知方程
有唯一实数解,由参变量分离法得知方程![]() 有唯一解(其中
有唯一解(其中![]() ),构造函数
),构造函数![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性与极值,利用数形结合思想可得出正实数
的单调性与极值,利用数形结合思想可得出正实数![]() 的值.
的值.
(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)当![]() ,
,![]() 时,
时,![]() ,
,
由于![]() ,由题意知,方程
,由题意知,方程![]() 有唯一实数解,则方程
有唯一实数解,则方程![]() 有唯一解,
有唯一解,
构造函数![]() ,其中
,其中![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() .
.
因为函数![]() 在其定义域上为减函数 ,
在其定义域上为减函数 ,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
所以,函数![]() 的极小值为
的极小值为![]() ,作出函数
,作出函数![]() 和
和![]() 的图象如下图所示:
的图象如下图所示:

![]() ,则
,则![]() ,由图象可知,当
,由图象可知,当![]() 时,即当
时,即当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象只有一个交点,因此,
的图象只有一个交点,因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图1,四棱锥![]() 中,
中,![]() 底面
底面![]() ,面
,面![]() 是直角梯形,
是直角梯形,![]() 为侧棱
为侧棱![]() 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示.

(1)证明:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点![]() ,并求
,并求![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。
(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年福建省高考实行“![]() ”模式.“
”模式.“![]() ”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
(1)若学生甲在“1”中选物理,在“2”中任选2科,求学生甲选化学和生物的概率;
(2)若学生乙在“1”中任选1科,在“2”中任选2科,求学生乙不选政治但选生物的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动,旨在全面提高国民体质和健康水平.某部门在该市2013-2018年发布的全民健身指数中,对其中的“运动参与评分值![]() ”(满分100分)进行了统计,制成如图所示的散点图.
”(满分100分)进行了统计,制成如图所示的散点图.
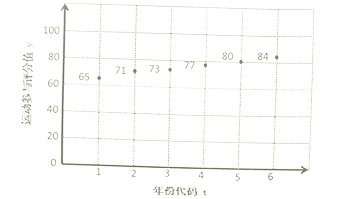
(1)根据散点图,建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)从该市的市民中随机抽取了容量为150的样本,其中经常参加体育锻炼的人数为50,以频率为概率,若从这150名市民中随机抽取4人,记其中“经常参加体育锻炼”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为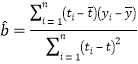 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,过动点M(0,m)的直线交x轴于点N,交椭圆C于A,P(其中P在第一象限,N在椭圆内),且M是线段PN的中点,点P关于x轴的对称点为Q,延长QM交C于点B,记直线PM,QM的斜率分别为k1,k2.
,过动点M(0,m)的直线交x轴于点N,交椭圆C于A,P(其中P在第一象限,N在椭圆内),且M是线段PN的中点,点P关于x轴的对称点为Q,延长QM交C于点B,记直线PM,QM的斜率分别为k1,k2.
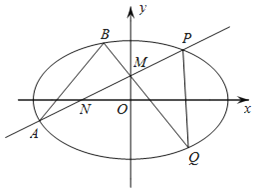
(1)当![]() 时,求k2的值;
时,求k2的值;
(2)当![]() 时,求直线AB斜率的最小值.
时,求直线AB斜率的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com