
| A. | 1 | B. | -1 | C. | i | D. | -i |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
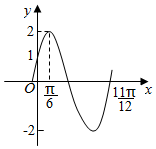 已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.
已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
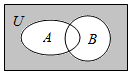 设全集U=R,集合A={x|-4<x<1},B={x|${4}^{x+\frac{1}{2}}$>$\frac{1}{8}$},则图中阴影部分所表示的集合为(-∞,-4].
设全集U=R,集合A={x|-4<x<1},B={x|${4}^{x+\frac{1}{2}}$>$\frac{1}{8}$},则图中阴影部分所表示的集合为(-∞,-4].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | B. | (-5,1) | ||
| C. | (-5,-1) | D. | (-5,-1)∪(-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆 .
.
(Ⅰ)若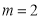 ,求椭圆
,求椭圆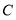 的离心率及短轴长;
的离心率及短轴长;
(Ⅱ)如存在过点 ,且与椭圆
,且与椭圆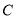 交于
交于 两点的直线
两点的直线 ,使得以线段
,使得以线段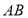 为直径的圆恰好通过坐标原点,求
为直径的圆恰好通过坐标原点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:解答题
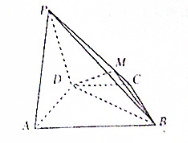
如图,在四棱锥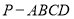 中,平面
中,平面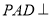 平面
平面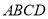 ,
,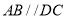 ,
,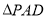 是等边三角形.已知
是等边三角形.已知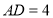 ,
,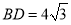 ,
,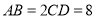 .
.
(1)设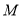 是
是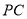 上的一点,证明:平面
上的一点,证明:平面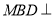 平面
平面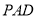 ;
;
(2)当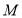 点位于线段
点位于线段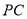 什么位置时,
什么位置时,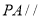 平面
平面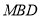 ?
?
(3)求四棱锥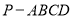 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com