【题目】抛掷一个质地均匀的骰子的试验，事件A表示“小于5的偶数点出现”，事件B表示“不小于5的点数出现”，则一次试验中，事件A或事件B至少有一个发生的概率为（ ）
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】如图是一个几何体的平面展开图，其中四边形
为正方形，
，
，
，
为全等的等边三角形，
、
分别为
、
的中点，在此几何体中，下列结论中正确的个数有（）
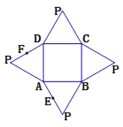
①平面
平面
②直线
与直线
是异面直线
③直线与直线
共面
④面与面
的交线与
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场销售某种商品的经验表明，该商品每日的销售量
(单位：千克)与销售价格
(单位：元/千克)满足关系式
，其中
为常数.已知销售价格为5元/千克时，每日可售出该商品13千克.
（1）求
的值；
（2）若该商品的成本为3元/千克，试确定销售价格的值，使商场每日销售该商品所获得的利润最大，并求出最大利润.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当
时，求
的极值；
（2）当
时，若函数恰有两个不同的零点，求
的值；
（3）当
时，若
的解集为
，且 中有且仅有一个整数，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的定义域为
，部分对应值如下表，的导函数
的图象如图所示．
|
|
|
|
|
|
|
|
|
|
下列关于的命题：
①函数的极大值点为
；
②函数在
上是减函数；
③如果当
时，的最大值是
，那么
的最大值为
；
④当
时，函数
有个零点；
⑤函数的零点个数可能为
、
、、
、个．
其中正确命题的个数是（ ）
A. B. C. D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某次文艺汇演，要将A、B、C、D、E、F这六个不同节目编排成节目单，如下表：
如果A、B两个节目要相邻，且都不排在第3号位置，则节目单上不同的排序方式有（ ）种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校响应教育部门疫情期间“停课不停学”的号召，实施网络授课，为检验学生上网课的效果，高三学年进行了一次网络模拟考试.全学年共1500人，现从中抽取了100人的数学成绩，绘制成频率分布直方图(如图所示).已知这100人中
分数段的人数比
分数段的人数多6人.
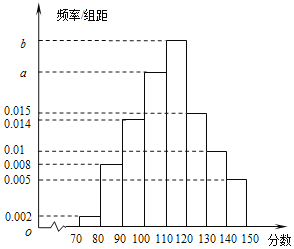
（1）根据频率分布直方图，求a，b的值，并估计抽取的100名同学数学成绩的中位数；(中位数保留两位小数)
（2）现用分层抽样的方法从分数在
，
的两组同学中随机抽取6名同学，从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言，求这2名同学的分数不在同一组内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，四边形
是边长为2的正方形，
，
为
的中点，点
在
上，
平面
，
在
的延长线上，且
.
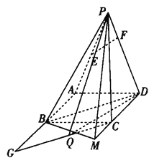
(1)证明:
平面
.
(2)过点
作
的平行线，与直线
相交于点
，点
为
的中点，求到平面
的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在班级活动中，4名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答）
（1）三名女生不能相邻，有多少种不同的站法？
（2）四名男生相邻有多少种不同的排法？
（3）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？
（4）甲乙丙三人按高低从左到右有多少种不同的排法？（甲乙丙三位同学身高互不相等）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
