
【题目】如图所示,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.
中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为
为![]() 中点,求平面
中点,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出春夏两句的有45人,能说出春夏秋三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出第一句“春”或一句也说不出的大约有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生“新型冠状病毒”肺炎疫情,国家卫健委紧急部署,从多省调派医务工作者前去支援,正值农历春节举家团圆之际,他们成为“最美逆行者”.武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者疑似的新冠肺炎患者无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户不漏一人.若在排查期间,某小区有5人被确认为“确诊患者的密切接触者”,现医护人员要对这5人随机进行逐一“核糖核酸”检测,只要出现一例阳性,则将该小区确定为“感染高危小区”.假设每人被确诊的概率均为![]() 且相互独立,若当
且相互独立,若当![]() 时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则
时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则![]() ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过![]() 的部分按照平价收费,超过
的部分按照平价收费,超过![]() 的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组
的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组![]() 制作了频率分布直方图,
制作了频率分布直方图,
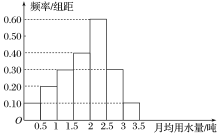
(1)从频率分布直方图中估计该40位居民月均用水量的众数,中位数;
(2)在该样本中月均用水量少于1吨的居民中随机抽取两人,其中两人月均用水量都不低于0.5吨的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R).
R).
(1)当b=﹣1时,函数![]() 有两个极值,求a的取值范围;
有两个极值,求a的取值范围;
(2)当a+b=1时,函数![]() 的最小值为2,求a的值;
的最小值为2,求a的值;
(3)对任意给定的正实数a,b,证明:存在实数![]() ,当
,当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
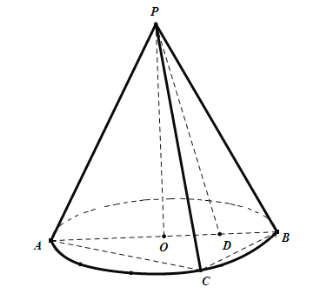
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019年亚洲杯前,某商家为了鼓励中国球迷组团到阿联酋支持中国队,制作了3种精美海报,每份中国队球迷礼包中随机装入一份海报,每集齐3种不同的海报就可获得中国队在亚洲杯上所有比赛中的1张门票.现有6名中国队球迷组成的球迷团,每人各买一份中国队球迷礼包,则该球迷团至少获得1张门票的可能情况的种数为( )
A.360B.450C.540D.990
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com