
判断方程
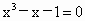 在区间[1,1.5]内有无实数解;如果有,求出一个近似解(精确到0.1).
在区间[1,1.5]内有无实数解;如果有,求出一个近似解(精确到0.1).
|
设函数  ,因为f(1)=-1<0,f(1.5)=0.875>0,且函数 ,因为f(1)=-1<0,f(1.5)=0.875>0,且函数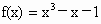 的图象是连续的曲线,所以方程 的图象是连续的曲线,所以方程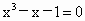 在区间[1,1.5]内有实数解. 在区间[1,1.5]内有实数解.
取区间 (1,1.5)的中点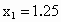 ,用计算器可算得f(1.25)=-0.30<0.因为f(1.25)·f(1.5)<0,所以 ,用计算器可算得f(1.25)=-0.30<0.因为f(1.25)·f(1.5)<0,所以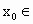 (1.25,1.5). (1.25,1.5).
再取 (1.25,1.5)的中点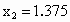 ,用计算器可算得f(1.375)≈0.22>0.因为f(1.25)·f(1.375)<0,所以 ,用计算器可算得f(1.375)≈0.22>0.因为f(1.25)·f(1.375)<0,所以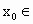 (1.25,1.375). (1.25,1.375).
同理,可得 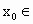 (1.3125,1.375), (1.3125,1.375),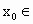 (1.3125,1.34375). (1.3125,1.34375).
由于 |1.34375-1.3125|<0.1,此时区间 (1.3125,1.34375)的两个端点精确到0.1的近似值都是1.3,所以方程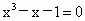 在区间[1,1.5]精确到0.1的近似解约为1.3. 在区间[1,1.5]精确到0.1的近似解约为1.3.
|


科目:高中数学 来源: 题型:
下面是函数f(x)在区间[1,2]上的一些点的函数值
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| g(x)+3x+1 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分16分)
已知向量![]()
![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]()
![]() ,与
,与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(3)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com