
【题目】已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)当![]() 时,记函数
时,记函数![]() 的所有单调递增区间的长度为
的所有单调递增区间的长度为![]() ,所有单调递减区间的长度为
,所有单调递减区间的长度为![]() ,证明:
,证明:![]() .(注:区间长度指该区间在
.(注:区间长度指该区间在![]() 轴上所占位置的长度,与区间的开闭无关.)
轴上所占位置的长度,与区间的开闭无关.)
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】数列{![]() }的前
}的前![]() 项和为Sn,且Sn=n(n+1)(n∈N*).
项和为Sn,且Sn=n(n+1)(n∈N*).
(1)若数列![]() 满足:
满足:![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列{
,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
(3)![]()
![]() ,(n为正整数),问是否存在非零整数
,(n为正整数),问是否存在非零整数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有![]() 若存在,求
若存在,求![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
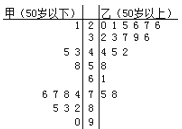
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每轮游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每轮游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓是否出现音乐相互独立.
,且各次击鼓是否出现音乐相互独立.
(1)玩三轮游戏,至少有一轮出现音乐的概率是多少?
(2)设每轮游戏获得的分数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,离心率为
,离心率为![]() ,已知过
,已知过![]() 轴上一点
轴上一点![]() 作一条直线
作一条直线![]() :
:![]() ,交椭圆于
,交椭圆于![]() 两点,且
两点,且![]() 的周长最大值为8.
的周长最大值为8.
(1)求椭圆方程;
(2)以点![]() 为圆心,半径为
为圆心,半径为![]() 的圆的方程为
的圆的方程为![]() .过
.过![]() 的中点
的中点![]() 作圆的切线
作圆的切线![]() ,
,![]() 为切点,连接
为切点,连接![]() ,证明:当
,证明:当![]() 取最大值时,点
取最大值时,点![]() 在短轴上(不包括短轴端点及原点).
在短轴上(不包括短轴端点及原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
位居民2017年12月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是
五组,整理得到如下的频率分布直方图,则下列说法错误的是

A. ![]() 月份人均用电量人数最多的一组有
月份人均用电量人数最多的一组有![]() 人
人
B. ![]() 月份人均用电量不低于
月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. ![]() 月份人均用电量为
月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了 30 名同学,得到如下的 ![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用学习成绩优秀的 12 名同学中,随机抽取 2 名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中倍抽取的 5 名同学,再随机抽取 3 名同学,试求抽取 3 名同学中恰有 2 名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某班级50名学生订阅数学、语文、英语学习资料的情况,其中A表示订阅数学学习资料的学生,B表示订阅语文学习资料的学生,C表示订阅英语学习资料的学生

(1)从这个班任意选择一名学生,用自然语言描述1,4,5,8各区域所代表的事件;
(2)用A,B,C表示下列事件:
①恰好订阅一种学习资料;
②没有订阅任何学习资料.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com