
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2列联表:
2列联表:| | 会围棋 | 不会围棋 | 总计 |
| 男 | | | |
| 女 | | | |
| 总计 | | | 30 |
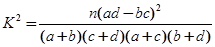 其中n=a+b+c+d
其中n=a+b+c+d | 0.40 | 0.25 | 0.10 | 0.010 |
 | 0.708 | 1.323 | 2.706 | 6.635 |
 ,求
,求 的期望.
的期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
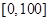 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
. 的值;
的值; ,求
,求 的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 视觉 视觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 |  | |
| 偏高 | 2 |  | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
 .
. 、
、 的值;
的值; ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
 的数学期望;
的数学期望;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com